题目内容
5.若关于x的方程(k-1)x2+2x-2=0有实数根,则k的取值范围是k≥$\frac{1}{2}$.分析 分二次项系数为零及二次项系数非零两种情况考虑,当k-1=0时,通过解一元一次方程可得出方程有解,即k=1符合题意;当k-1≠0时,由根的判别式△≥0,可求出k的取值范围.综上即可得出结论.
解答 解:当k-1=0,即k=1时,原方程为2x-2=0,
解得:x=1,
∴k=1符合题意;
当k-1≠0,即k≠-1时,有△=22-4×(k-1)×(-2)≥0,
解得:k≥$\frac{1}{2}$且k≠1.
综上所述:k的取值范围是k≥$\frac{1}{2}$.
故答案为:k≥$\frac{1}{2}$.
点评 本题考查了根的判别式以及解一元一次方程,分二次项系数为零及二次项系数非零两种情况考虑是解题的关键.

练习册系列答案
相关题目
13. 下图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
下图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
 下图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
下图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 南 | D. | 江 |
20. 以如图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换,不能得到图(2)的是( )
以如图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换,不能得到图(2)的是( )
 以如图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换,不能得到图(2)的是( )
以如图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换,不能得到图(2)的是( )| A. | 绕着OB的中点旋转180°即可 | |
| B. | 只要向右平移1个单位 | |
| C. | 先以直线AB为对称轴进行翻折,再向右平移1个单位 | |
| D. | 先绕着点O旋转180°,再向右平移1个单位 |
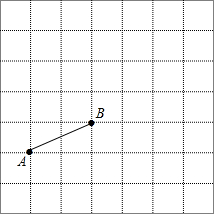 如图,已知A(-1,0),B(1,1),把线段AB平移,使点B落在点D(3,4)处,这时点A移动到点C处.
如图,已知A(-1,0),B(1,1),把线段AB平移,使点B落在点D(3,4)处,这时点A移动到点C处.