题目内容
 (2013•澄海区模拟)钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为12海里(即MC=12海里).在A点测得岛屿的西端点M在点A的东北方向;航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东60°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离.
(2013•澄海区模拟)钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为12海里(即MC=12海里).在A点测得岛屿的西端点M在点A的东北方向;航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东60°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离.分析:在直角△ACM,∠CAM=45度,则△ACM是等腰直角三角形,即可求得AC的长,则BC可以求得,然后在直角△BCN中,利用三角函数求得AN,根据MN=CN-CM即可求解.
解答:解:在直角△ACM,∠CAM=45度,则△ACM是等腰直角三角形,
则AC=CM=12(海里),
∴BC=AC-AB=12-4=8(海里),
直角△BCN中,CN=BC•tan∠CBN=
BC=8
(海里),
∴MN=CN-CM=8
-12(海里).
答:钓鱼岛东西两端点MN之间的距离是8
-12海里.
则AC=CM=12(海里),
∴BC=AC-AB=12-4=8(海里),
直角△BCN中,CN=BC•tan∠CBN=
| 3 |
| 3 |
∴MN=CN-CM=8
| 3 |
答:钓鱼岛东西两端点MN之间的距离是8
| 3 |
点评:本题考查了三角函数,正确求得BC的长度是关键.

练习册系列答案
相关题目
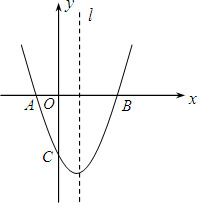 (2013•澄海区模拟)如图,已知在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴分别交于A、B两点,与y轴交于点C.
(2013•澄海区模拟)如图,已知在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴分别交于A、B两点,与y轴交于点C.