题目内容
如图，圆内接四边形ABCD中，圆心角∠1=100°，则圆周角∠ABC等于
- A.100°
- B.120°
- C.130°
- D.150°
C
分析：先根据圆周角定理求出∠ADC的度数，再根据圆内接四边形的性质求出∠ABC的度数即可．
解答：∵圆心角∠1=100°，
∴∠ADC=
∠1=50°，
∵四边形ABCD是圆内接四边形，
∴∠ABC=180°-∠ADC=180°-50°=130°．
故选C．
点评：此类题目比较简单，考查的是圆周角定理及圆内接四边形的性质．
分析：先根据圆周角定理求出∠ADC的度数，再根据圆内接四边形的性质求出∠ABC的度数即可．
解答：∵圆心角∠1=100°，
∴∠ADC=
∠1=50°，∵四边形ABCD是圆内接四边形，
∴∠ABC=180°-∠ADC=180°-50°=130°．
故选C．
点评：此类题目比较简单，考查的是圆周角定理及圆内接四边形的性质．
练习册系列答案
口算能手系列答案
相关题目
11、如图，圆内接四边形ABCD的对角线AC，BD把四边形的四个内角分成八个角，这八个角中相等的角的对数至少有（ ）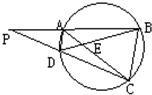
15、如图，圆内接四边形ABCD的BA，CD的延长线交于P，AC，BD交于E，则图中相似三角形有（ ）
2、已知：如图，圆内接四边形ABCD中，∠BAD=65°，则∠BCD=
已知：如图，圆内接四边形ABCD，过C点作对角线BD的平行线交AD的延长线于E点．
如图，圆内接四边形ABCD，AB=AD，∠BAD=60°，AC=2，则四边形ABCD的面积为（ ）| A、4 | ||
| B、2 | ||
C、
| ||
D、
|