Question

【题目】在一次数学探究活动课中，某同学有一块矩形纸片，已知，，为射线上的一个动点，将沿折叠得到，若是直角三角形，则所有符合条件的点所对应的的和为__________．

Answer 1

【答案】26

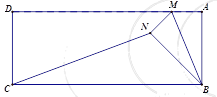
【解析】分析：根据轴对称的性质分别画出点M在线段AD上和AD的延长线上时的图形，结合勾股定理列方程.

详解：因为∠NCB＜90°，∠NBC＜90°，所以∠BNC＝90°.

①如图1，当点M在线段AD上时，由轴对称的性质得，MN＝MA，

设MN＝MA＝x，

Rt△CBN中，由勾股定理得CN＝12，

Rt△MCD中，由勾股定理得，52＋(13－x)2＝(12＋x)2，解得x＝1.

①如图2，当点M在线段AD延长线上时，因为∠BNM＝90°，又∠BNC＝90°，所以点M，C，N在一条直线上，由轴对称的性质得，MN＝MA，

设MN＝MA＝x，

Rt△CBN中，由勾股定理得CN＝12，

Rt△MCD中，由勾股定理得，52＋(x－13)2＝(x－12)2，解得x＝25.

则1＋25＝26.

故答案为26.