题目内容
9.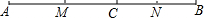 如图.点C是线段AB上一点,点M.N分别是线段AC、BC的中点.
如图.点C是线段AB上一点,点M.N分别是线段AC、BC的中点.(1)若线段AC=6,BC=4,求线段MN的长;
(2)若AC+BC=a,求线段MN的长;
(3)题目中“点C是线段AB上”,若改为“点C是直线AB上”,(1)中结果会变吗?若有变.请求线段MN的长.
分析 (1)根据点M、N分别是AC、BC的中点,先求出CM、CN的长度,则MN=CM+CN;
(2)根据点M、N分别是AC、BC的中点,CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,所以MN=$\frac{1}{2}$(AC+BC)=$\frac{a+b}{2}$;
(3)长度会发生变化,分点C在线段AB上、点B在A、C之间和点A在B、C之间三种情况讨论.
解答 解:(1)∵AC=6,点M是AC的中点
∴CM=$\frac{1}{2}$AC=3cm
∵BC=4,点N是BC的中点
∴CN=$\frac{1}{2}$BC=2,
∴MN=CM+CN=5,
∴线段MN的长度为5.
(2)MN=$\frac{a+b}{2}$.
(3)线段MN的长度会变化.
当点C在线段AB上时,由(2)知MN=$\frac{a+b}{2}$,
当点C在线段AB的延长线时,如图1:
则AC=a>BC=b,
∵AC=a点M是AC的中点,
∴CM=$\frac{1}{2}$AC=$\frac{1}{2}$a,
∵BC=b点N是BC的中点
∴CN=$\frac{1}{2}$BC=$\frac{1}{2}$b,
∴MN=CM-CN=$\frac{a-b}{2}$,
当点C在线段BA的延长线时,如图2: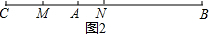 ,
,
则AC=a<BC=b
同理可求:CM=$\frac{1}{2}$AC=$\frac{1}{2}$a,
CN=$\frac{1}{2}$BC=$\frac{1}{2}$b,
∴MN=CN-CM=$\frac{b-a}{2}$,
综上所述,线段MN的长度会变化,MN=$\frac{a+b}{2}$,$\frac{a-b}{2}$,$\frac{b-a}{2}$.
点评 本题主要是线段中点的运用,分情况讨论是解题的难点,难度较大.

 将如图折叠成正方体后,与“七”字相对面上的汉字是( )
将如图折叠成正方体后,与“七”字相对面上的汉字是( )| A. | 育 | B. | 才 | C. | 学 | D. | 校 |
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
| A. | ( 2,-3) | B. | (-2,3) | C. | (2,3) | D. | (-2,-3) |
| A. | ①②③④⑤ | B. | ②④ | C. | ①③⑤ | D. | ②④⑤ |

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |