��Ŀ����
����Ŀ�����ı�����ABCD����EΪAB���ϵ�һ�㣬��FΪ�Խ���BD�ϵ�һ�㣬��EF��AB��
��1�����ı���ABCDΪ�����Σ�
����ͼ1����ֱ��д��AE��DF��������ϵ��
�ڽ���EBF�Ƶ�B��ʱ����ת��ͼ2��ʾ��λ�ã�����AE��DF������AE��DF��������ϵ��˵�����ɣ�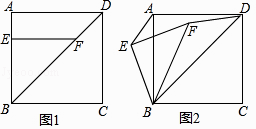
��2����ͼ3�����ı���ABCDΪ���Σ�BC=mAB���������������䣬����EBF�Ƶ�B˳ʱ����ת����0�㣼����90�㣩�õ���E'BF'������AE'��DF'������ͼ3�л�����ͼ����ֱ��д��AE'��DF'��������ϵ��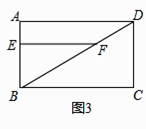
���𰸡�
��1��[ "��DF= ![]() AE
AE
�ڽ�:�������£�
�ߡ�EBF�Ƶ�B��ʱ����ת��ͼ2��ʾ��λ�ã�
���ABE=��DBF��
�� ![]() =
= ![]() ��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
���ABE�ס�DBF��
�� ![]() =
= ![]() =
= ![]() ��
��
��DF= ![]() ��2��
��2��
�⣺��ͼ3��
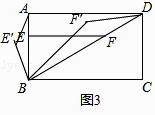
���ı���ABCDΪ���Σ�
��AD=BC=mAB��
��BD= ![]() =
= ![]() AB��
AB��
��EF��AB��
��EF��AD��
���BEF�ס�BAD��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() =
= ![]() ��
��
�ߡ�EBF�Ƶ�B˳ʱ����ת����0�㣼����90�㣩�õ���E'BF'��
���ABE��=��DBF�䣬BE��=BE��BF��=BF��
�� ![]() =
= ![]() =
= ![]() ��
��
���ABE��ס�DBF�䣬
�� ![]() =
= ![]() =
= ![]() ��
��
��DF��= ![]() AE�䣮
AE�䣮
���������⣺��1���١��ı���ABCDΪ�����Σ�
���ABDΪ����ֱ�������Σ�
��BF= ![]() AB��
AB��
��EF��AB��
���BEFΪ����ֱ�������Σ�
BF= ![]() BE��
BE��
��BD��BF= ![]() AB��
AB�� ![]() BE��
BE��
��DF= ![]() AE��
AE��
���Դ���DF= ![]() AE��
AE��

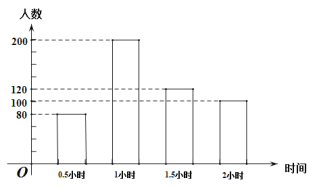
����Ŀ������ʦΪ���˽�ѧ�������ڼҵ��Ķ���������������20��ѧ��ijһ����Ķ�Сʱ�����������ͳ�����£�
�Ķ�ʱ�� | 2 | 2.5 | 3 | 3.5 | 4 |
ѧ������������ | 1 | 2 | 8 | 6 | 3 |
�������20��ѧ���Ķ�Сʱ����˵����ȷ���ǣ� ��
A.������8
B.�����3
C.ƽ������3
D.������0.34