Question

【题目】已知：内接于，弦，垂足为，连接．

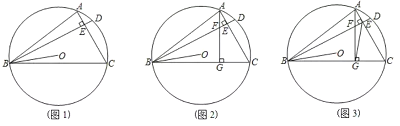
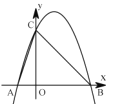
（1）如图1，求证：；

（2）如图2，过点作，垂足为，交于点，求证：；

（3）如图3，在（2）的条件下，连接、，且，若，，求的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）．

【解析】

（1）延长BO 交⊙O 于点M，连接CM，由圆周角定理可得∠BCM=90°，由余角的性质可得结论；

（2）连接AD，由同弧所对圆周角相等可知∠ADB=∠ACB，根据AD⊥AC于，AG⊥BC，可得∠AFE=∠ACB=90°-∠GAC，所以∠AFE=∠ADE，因此AF=AD，从而得出结论EF=ED；

（3）延长AG交⊙O于N，连接BN，DN，作DH⊥BC于H．由（2）同理可得FG=GN，BF=BN，∠FBG=∠NBG，由（2）知EF=DE，得出DN=2EG=30，设∠ABD=∠OBC=∠ACD=3α，推出∠DCB=2∠DBC，∠DBN=∠DNB=∠DCB=60°+2α，所以DB=DN=30．设CH=x，则BH=x+18，由勾股定理302-（x+18）2=182-x2，解得x=7，得出BH=25，BC=32，再根据cos∠DBC=，求出BE=．

解：（1）延长交于，连接．

∵是直径

∴

又∵

∴

∵于

∴

∴，

∴

（2）连接，

∵

∴

∵于，于

∴

∴

∴

∴

（3）延长交于，连接，，作于

由（2）同理可得，，

由（2）知

∴为的中位线

∴

设

计算，

∴∴

再计算

∴

在2倍角中，

∵于

∴

设，则

∵

∴

解得，，，

∴

∴．