题目内容
 已知有理数a、b、c在数轴上的位置如图所示.化简:|a+b|-|c-b|+|c-a|.
已知有理数a、b、c在数轴上的位置如图所示.化简:|a+b|-|c-b|+|c-a|.考点:整式的加减,数轴,绝对值
专题:
分析:先根据各点在数轴上的位置判断出其符号,再根据绝对值的性质去绝对值符号,合并同类项即可.
解答:解:∵由图可知,c<a<b,|a|<b,|c|>b>|a|,
∴a+b>0,c-b<0,c-a<0,
∴原式=a+b-(b-c)+(a-c)
=a+b-b+c+a-c
=2a.
∴a+b>0,c-b<0,c-a<0,
∴原式=a+b-(b-c)+(a-c)
=a+b-b+c+a-c
=2a.
点评:本题考查的是整式的加减,熟知整式的加减实质上就是合并同类项是解答此题的关键.

练习册系列答案
相关题目
下列各题正确的是( )
| A、3x+3y=6xy |
| B、x+x=x2 |
| C、-9y2+6y2=-3 |
| D、9a2b-9a2b=0 |
-3的倒数的绝对值是( )
A、
| ||
B、-
| ||
| C、3 | ||
| D、±3 |
 如图,直角三角形ABC中,∠C=90°,D为AC上一点,DA=DB=5,△ABD的面积为10,则CD长是( )
如图,直角三角形ABC中,∠C=90°,D为AC上一点,DA=DB=5,△ABD的面积为10,则CD长是( )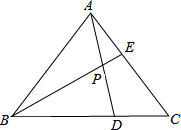 已知如图,在△ABC的边BC,AC上分别取点D、E,使BD=2CD,CE=2AE,AD与BE的交点为P,求证:S△EPA:S△APB:S△BPD:S△ABC=1:6:8:21.
已知如图,在△ABC的边BC,AC上分别取点D、E,使BD=2CD,CE=2AE,AD与BE的交点为P,求证:S△EPA:S△APB:S△BPD:S△ABC=1:6:8:21.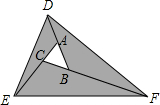 如图,已知△ABC,现将边BA延长至点D,使AD=AB,延长AC至点E,使CE=2AC.延长CB至点F,使BF=3BC,分别连结DE,DF,EF,得到△DEF,若△ABC的面积为1,则阴影部分的面积为
如图,已知△ABC,现将边BA延长至点D,使AD=AB,延长AC至点E,使CE=2AC.延长CB至点F,使BF=3BC,分别连结DE,DF,EF,得到△DEF,若△ABC的面积为1,则阴影部分的面积为