题目内容
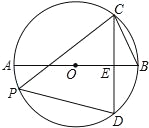
如图，⊙O的直径AB⊥弦CD，垂足为点E，点P在优弧CAD上（不包含点C和点D），连PC、PD、CB，tan∠BCD=
．
（1）求证：AE=CD；
（2）求sin∠CPD．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
智趣寒假作业云南科技出版社系列答案题目内容
如图，⊙O的直径AB⊥弦CD，垂足为点E，点P在优弧CAD上（不包含点C和点D），连PC、PD、CB，tan∠BCD=．
（1）求证：AE=CD；
（2）求sin∠CPD．
智趣寒假作业云南科技出版社系列答案
），四边形OCBA是平行四边形，点M（t，0）为x轴正半轴上的点，点N为射线AB上的点，且AN=OM，点D为抛物线的顶点．
AB为半径作弧，连接弧的交点得到直线l，在直线l上取一点C，使得∠CAB＝25°，延长AC至点M，则∠BCM的度数为( )
B. 
C. 
D. 
，将此函数的图象记为P．若直线y=x+b与图形P恰有两个公共点，则b的值为_____．
﹣（3.14﹣π）0﹣|1﹣
|．