题目内容
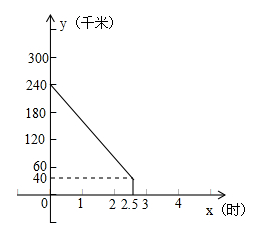
南京至上海的沪宁高速公路长约300千米.甲、乙两车同时分别从距南京240千米、60千米的入口行驶上沪宁高速公路.甲车驶往南京、乙车驶往上海.甲车在行驶过程中速度始终不变.甲车离南京(沪宁高速公路南京起点)的距离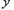 (千米)与行驶时间
(千米)与行驶时间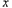 (时)之间的函数图像如图所示.
(时)之间的函数图像如图所示.
(1)求出甲车离南京的距离)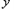 (千米)与行驶时间
(千米)与行驶时间 (时)之间的函数表达式;
(时)之间的函数表达式;
(2)乙车若以60千米/时的速度匀速行驶,1小时后两车相距多少千米?
(3)乙车按(2)中状态行驶与甲车相遇后,速度改为a千米/时,结果两车同时到达沪宁高速南京、上海起点,求乙车变化后的速度a;并在如图所示的直角坐标系中,画出乙车离南京的距离)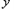 (千米)与行驶时间
(千米)与行驶时间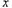 (时)之间的函数图像
(时)之间的函数图像
解:(1)设 =k
=k +b,把点(2.5,40)和(0,240)代人求得
+b,把点(2.5,40)和(0,240)代人求得 =
= 80,b=240,
80,b=240,
因此, .
.
(2)由题意得 ,当
,当 =1时,
=1时, =160,
=160, =120,
=120, 40(千米).
40(千米).
(3)根据两车相遇,得: ,即
,即 80
80 + 240= 60
+ 240= 60 + 60,
+ 60,
解得 ,代入得
,代入得 ,
,
两直线交点坐标为( ,
, ).令
).令 ,即
,即 80
80 +240=0,解得
+240=0,解得 =3,
=3,
当 =3时,
=3时, ,
,
因此 .
.
其函数图像如下图.
 =k
=k +b,把点(2.5,40)和(0,240)代人求得
+b,把点(2.5,40)和(0,240)代人求得 =
= 80,b=240,
80,b=240,因此,
 .
.(2)由题意得
 ,当
,当 =1时,
=1时, =160,
=160, =120,
=120, 40(千米).
40(千米).(3)根据两车相遇,得:
 ,即
,即 80
80 + 240= 60
+ 240= 60 + 60,
+ 60,解得
 ,代入得
,代入得 ,
,两直线交点坐标为(
 ,
, ).令
).令 ,即
,即 80
80 +240=0,解得
+240=0,解得 =3,
=3,当
 =3时,
=3时, ,
,因此
 .
.其函数图像如下图.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
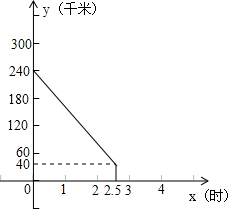 南京至上海的沪宁高速公路长约300千米.甲、两车同时分别从距南京240千米、60千米的入口行驶上沪宁高速上正常行驶.甲车驶往南京、乙车驶往上海.甲车在行驶过程中速度始终不变.甲车离南京(沪宁高速公路南京起点)的距离y(千米)与行驶时间x(时)之间的函数图象如图所示.
南京至上海的沪宁高速公路长约300千米.甲、两车同时分别从距南京240千米、60千米的入口行驶上沪宁高速上正常行驶.甲车驶往南京、乙车驶往上海.甲车在行驶过程中速度始终不变.甲车离南京(沪宁高速公路南京起点)的距离y(千米)与行驶时间x(时)之间的函数图象如图所示.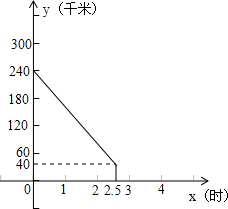 南京至上海的沪宁高速公路长约300千米.甲、两车同时分别从距南京240千米、60千米的入口行驶上沪宁高速上正常行驶.甲车驶往南京、乙车驶往上海.甲车在行驶过程中速度始终不变.甲车离南京(沪宁高速公路南京起点)的距离y(千米)与行驶时间x(时)之间的函数图象如图所示.
南京至上海的沪宁高速公路长约300千米.甲、两车同时分别从距南京240千米、60千米的入口行驶上沪宁高速上正常行驶.甲车驶往南京、乙车驶往上海.甲车在行驶过程中速度始终不变.甲车离南京(沪宁高速公路南京起点)的距离y(千米)与行驶时间x(时)之间的函数图象如图所示.