题目内容
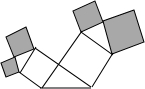 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的直角三角形斜边长为9cm,则四个阴影正方形的面积和是
如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的直角三角形斜边长为9cm,则四个阴影正方形的面积和是81
81
cm2.分析:根据勾股定理有S正方形1+S正方形2=l2,S正方形C+S正方形D=S正方形2,S正方形A+S正方形B=S正方形1,等量代换即可求四个阴影正方形的面积之和.
解答:解:如右图所示,

根据勾股定理可知,
S正方形1+S正方形2=l2,
S正方形C+S正方形D=S正方形2,
S正方形A+S正方形B=S正方形1,
∴S正方形C+S正方形D+S正方形A+S正方形B=l2=92=81.
故答案是:81.

根据勾股定理可知,
S正方形1+S正方形2=l2,
S正方形C+S正方形D=S正方形2,
S正方形A+S正方形B=S正方形1,
∴S正方形C+S正方形D+S正方形A+S正方形B=l2=92=81.
故答案是:81.
点评:本题考查了勾股定理的实际阴影,注意掌握两直角边的平方和等于斜边的平方,难度一般.

练习册系列答案
相关题目
按如图所示的规律用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,并解答下面问题: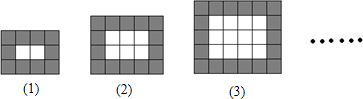
(1)将下表填写完整
| 图形编号 | (1) | (2) | (3) | (4) | … |
| 黑色瓷砖的块数 | 10 | 14 | 18 | ______ | … |
| 白色瓷砖的块数 | 2 | 6 | 12 | ______ | … |
(2)第(n)个图形中,共有黑色瓷砖______块,共有白色瓷砖______块;(用含n的代数式表示,答案直接写在题中横线上);
(3)如果每块黑色瓷砖12元每块白瓷砖10元,求购买铺设第(8)个图形所需瓷砖的费用;
(4)是否存在第(n)个图形,该图形所需白、黑瓷砖的总数为18325块?若存在,求出该图形的编号n;若不存在,请说明理由.
 16、如图所示的图形中,四边形CDEF是正方形,则x的值为
16、如图所示的图形中,四边形CDEF是正方形,则x的值为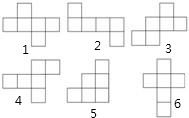 1、在如图所示的图形中是正方体的展开图的有( )
1、在如图所示的图形中是正方体的展开图的有( )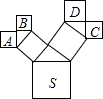 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积和是49cm2,则其中最大的正方形S的边长为
如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积和是49cm2,则其中最大的正方形S的边长为