题目内容
在矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF.
(1)求DE的长;
(2)连接BF,判断四边形BEDF的形状,并说明理由.

解:(1)由翻折不变性可知,EB=ED,
设DE为xcm,则EB=xcm,
∵AB=10cm,
∴AE=AB﹣x=10﹣x,
又∵AD=4cm,
∴在Rt△ADE中,AD2+AE2=DE2,即42+(10﹣x)2=x2,
化简得:16+100+x2﹣20x=x2,
解得:x=5.8,
即DE=5.8;
(2)连接BF,如下图所示,
∵AB∥CD,
∴∠BEF=∠DFE,
又∠BEF=∠DEF,
∴∠DFE=∠DEF,
∴DE=DF,
又DE=BE,
∴BE=DF,
∴四边形BEDF为菱形(有一组对边平行且相等的四边形为平行四边形,邻边相等的平行四边形是菱形).


练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
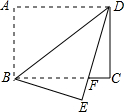 在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,求BF的长.
在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,求BF的长.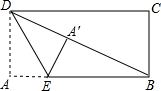 (2013•太原)如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为
(2013•太原)如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为 (2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;
(2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F; 如图,在矩形纸片ABCD中,AB=6,BC=8,现将其沿EF对折,使得点C与点A重合,则AF的长为
如图,在矩形纸片ABCD中,AB=6,BC=8,现将其沿EF对折,使得点C与点A重合,则AF的长为 动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.
动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.