题目内容
如图6,在四边形 中,
中,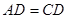 ,
, 平分
平分 ,
, ,
, .
.

(1)求证:四边形 是等腰梯形; (6分)
是等腰梯形; (6分)
(2)取边 的中点
的中点 ,联结
,联结 .求证:四边形
.求证:四边形 是菱形. (6分)
是菱形. (6分)
 中,
中,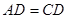 ,
, 平分
平分 ,
, ,
, .
.
(1)求证:四边形
 是等腰梯形; (6分)
是等腰梯形; (6分)(2)取边
 的中点
的中点 ,联结
,联结 .求证:四边形
.求证:四边形 是菱形. (6分)
是菱形. (6分)见解析
证明:(1)∵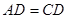 ,∴
,∴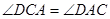
∵ 平分
平分 ,
,
∴
∴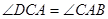 ,
,
∴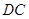 ∥
∥ (2分)
(2分)
在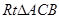 中,
中,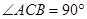 ,
,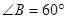
∴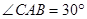 ,
,
∴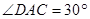 (1分)
(1分)
∴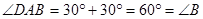 ,
,
∴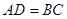 ………………(1分)
………………(1分)
∵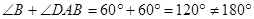
∴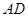 与
与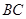 不平行, (1分)
不平行, (1分)
∴四边形 是等腰梯形. (1分)
是等腰梯形. (1分)
证明:(2)∵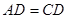 ,
,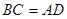 ,
,
∴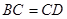 (1分)
(1分)
在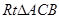 中,
中,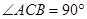 ,
,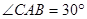
∴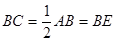 , (1分)
, (1分)
∴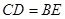 ,
,
∵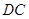 ∥
∥ (2分)
(2分)
∴四边形 是平行四边形 (1分)
是平行四边形 (1分)
∵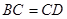
∴四边形 是菱形. (1分)
是菱形. (1分)
(1)由等腰三角形的性质、角平分线的性质利用等量代换可以推知内错角∠DCA=∠CAB,利用平行线的判定定理可以证得CD∥AB;然后由直角三角形的性质、角平分线的性质以及等腰三角形 判定定理知AD=BC;最后由等腰梯形的判定定理证得结论;
(2)根据菱形的判定定理(邻边相等的平行四边形是菱形)知,欲证四边形DEBC是菱形,首先证明四边形DEBC是平行四边形,然后结合(1)知邻边CD=BC
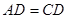 ,∴
,∴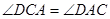
∵
 平分
平分 ,
,∴

∴
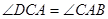 ,
,∴
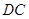 ∥
∥ (2分)
(2分)在
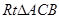 中,
中,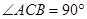 ,
,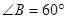
∴
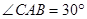 ,
,∴
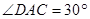 (1分)
(1分)∴
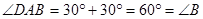 ,
,∴
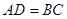 ………………(1分)
………………(1分)∵
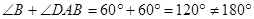
∴
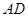 与
与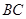 不平行, (1分)
不平行, (1分)∴四边形
 是等腰梯形. (1分)
是等腰梯形. (1分)证明:(2)∵
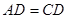 ,
,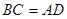 ,
,∴
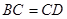 (1分)
(1分)在
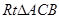 中,
中,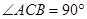 ,
,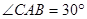
∴
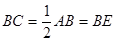 , (1分)
, (1分)∴
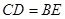 ,
,∵
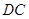 ∥
∥ (2分)
(2分)∴四边形
 是平行四边形 (1分)
是平行四边形 (1分)∵
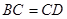
∴四边形
 是菱形. (1分)
是菱形. (1分)(1)由等腰三角形的性质、角平分线的性质利用等量代换可以推知内错角∠DCA=∠CAB,利用平行线的判定定理可以证得CD∥AB;然后由直角三角形的性质、角平分线的性质以及等腰三角形 判定定理知AD=BC;最后由等腰梯形的判定定理证得结论;
(2)根据菱形的判定定理(邻边相等的平行四边形是菱形)知,欲证四边形DEBC是菱形,首先证明四边形DEBC是平行四边形,然后结合(1)知邻边CD=BC

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ?
?

 ⑥
⑥ ,则等腰梯形的腰长是 cm.
,则等腰梯形的腰长是 cm.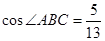 ,那么凉衣架两顶点
,那么凉衣架两顶点 、
、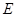 之间的距离为 cm.
之间的距离为 cm.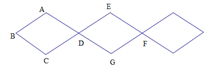
 中,
中, ,如果添加一个条件,即可判定该四边形是正方形,那么所添加的这个条件可以是( ).
,如果添加一个条件,即可判定该四边形是正方形,那么所添加的这个条件可以是( ). .
. ;
;  .
. ;
;  .
. ;
;  .
. .
. 
