题目内容

如图，AB为⊙O的直径，D为AB上一点，且AB=5AD，CD⊥AB，垂足为D，C在圆上，设∠COD=α，则sin $数学公式$ =________．

$\text{[math]}$
分析：由同弧所对的圆周角等于所对的圆心角的一半，得到所求式子的角 $\text{[math]}$ 与角B相等，求出sinB即可求出所求的，方法为：根据题中所给的条件设出AD=x，AB=5x，可将OD和OC的值表示出来，在直角三角形OCD中，根据勾股定理表示出CD，在直角三角形ADC中，再利用勾股定理表示出AC，最后在直角三角形ABC中，根据锐角三角函数的定义，即可求出sinB的值，即为所求sin $\text{[math]}$ 的值．
解答：设AD=x，则AB=5x，即⊙O的直径为5x，
∴OA=OC= $\text{[math]}$ ×5x= $\text{[math]}$ ，OD=OA-AD= $\text{[math]}$ ，
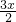∵AB为圆的直径，∴∠ACB=90°，
∵圆心角∠AOC=α与圆周角∠B所对的弧都为 $\text{[math]}$ ，
∴∠B= $\text{[math]}$ ∠AOC= $\text{[math]}$ ，
在Rt△OCD中，根据勾股定理得：CD²+OD²=OC²，
∴CD=2x，
在Rt△ACD中，AD=x，CD=2x，
根据勾股定理得：AC= $\text{[math]}$ x，
在Rt△ABC中，sinB=sin $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
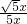点评：考查综合应用解直角三角形、直角三角形性质，进行逻辑推理能力和运算能力．