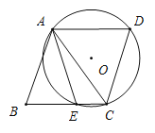��Ŀ����
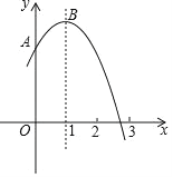
����Ŀ����ͼ��������y����x2��2x��m��1��mΪ��������y���ڵ�A����x���һ��������2��3֮�䣬����ΪB��
��������y����x2��2x��m��1��ֱ��y��m��2����ֻ��һ�����㣻
������M����2��y1������N��![]() ��y2������P��2��y3���ڸú���ͼ���ϣ���y1<y2<y3��
��y2������P��2��y3���ڸú���ͼ���ϣ���y1<y2<y3��
�۽�������������ƽ��2����λ��������ƽ��2����λ�����������߽���ʽΪy������x��1��2��m��
�ܵ�A����ֱ��x��1�ĶԳƵ�ΪC����D��E�ֱ���x���y���ϣ���m��1ʱ���ı���BCDE�ܳ�����СֵΪ![]() ��
��
������ȷ�ж��У� ��
A.�٢ڢۢ�B.�ڢۢ�C.�٢ۢ�D.�٢�
���𰸡�C
��������
�����κ����䷽��![]() �����жϢ٢ۣ���P���ݶԳ���ת�����Գ���������жϢڣ���m��1���뺯������ʽ��������A��C���꣬���ԳƸ�������֮���߶���̼��������ı���BCDE�ܳ�����Сֵ��
�����жϢ٢ۣ���P���ݶԳ���ת�����Գ���������жϢڣ���m��1���뺯������ʽ��������A��C���꣬���ԳƸ�������֮���߶���̼��������ı���BCDE�ܳ�����Сֵ��
�⣺��y����x2��2x��m��1��Ϊ����ʽΪ��![]()
�ඥ������Ϊ![]() ������ͼ����ֱ��y��m��2���У�ֻ��һ�������㣬����ȷ��
������ͼ����ֱ��y��m��2���У�ֻ��һ�������㣬����ȷ��
�������ϼ��¼�������Ҽ�����![]() ����ƽ��2����λ��������ƽ��2����λ�õ���
����ƽ��2����λ��������ƽ��2����λ�õ��� ![]() ������ȷ��
������ȷ��
���κ����ĶԳ�����ֱ��![]() ����P��2��y3���ɶԳƵ�
����P��2��y3���ɶԳƵ�![]() ���ڶԳ�����࣬y��x�����������
���ڶԳ�����࣬y��x�����������![]() ���ڴ���
���ڴ���
��m=1ʱ����������ʽΪ��![]() ����
����![]() ��
��![]() ��
��![]()
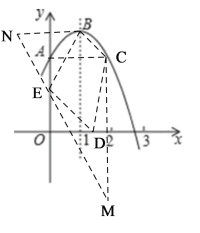
��B����y��ԳƵ�N����C����x��ԳƵ�M����![]() ����MN����MNΪBE��DE��CD�͵���Сֵ���ı���BCDE�ܳ���СֵΪMN��BC�ĺͣ����У�
����MN����MNΪBE��DE��CD�͵���Сֵ���ı���BCDE�ܳ���СֵΪMN��BC�ĺͣ����У�
![]()
�൱m��1ʱ���ı���BCDE�ܳ�����СֵΪ![]() ������ȷ��
������ȷ��
�ʴ�ѡ��C��

 ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�