Question

【题目】一副三角板直角顶点重合于点，，，．

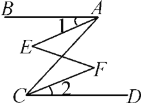
（1）如图（1），若，求证：；

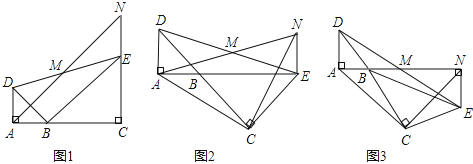
（2）如图（2），若,,则 度；

（3）如图（3），在（1）的条件下，与相交于点，连接，，若，，，求的面积．

Answer 1

【答案】（1）见解析；（2）165；（3）24

【解析】

（1）如图（1），证明∠E=∠ABE=30°，可得结论；
（2）如图（2），根据三角形的外角的性质可得∠AFE=∠A+∠ABE=α①，∠BGD=∠E+∠CBF=β②，①+②可得结论；
（3）如图（3），先根据三角形面积公式得：CG=BG，计算CG=2，BG=8，最后由三角形面积公式可得结论．

解：（1）证明：如图（1），∵∠AFE=75°，∠A=45°，
∴∠ABE=75°-45°=30°，
∵∠E=30°，
∴∠E=∠ABE，
∴AB∥DE；
（2）如图（2），△ABF中，∠AFE=∠A+∠ABE=α①，

△BGE中，∠BGD=∠E+∠CBF=β②，
①+②得：α+β=∠A+∠E+∠CBF+∠ABE=45°+30°+90°=165°；
故答案为：165；
（3）解：∵DE∥AB，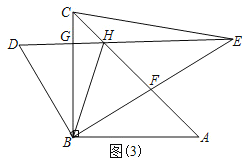

∴∠CGH=∠ABC=90°，
∵S△CEH=S△BEH，

∴EHCG＝EHBG，

∴CG=BG，
∵BC=10，
∴CG=2，BG=8，
∵DG=2CG=2GH，
∴DG=4，GH=2，
∴△BDH的面积=×DH×BG=×(2+4)×8=24．