题目内容
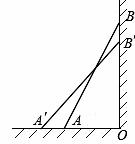
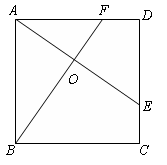
如图,在等腰梯形ABCD中,AB∥DC,线段AG,BG分别交CD于点E,F,DE=CF.求证:△GAB是等腰三角形.


见解析
证明:∵在等腰梯形中ABCD中,AD=BC,
∴∠D=∠C,∠DAB=∠CBA,
在△ADE和△BCF中,∵ ,∴△ADE≌△BCF(SAS)。
,∴△ADE≌△BCF(SAS)。
∴∠DAE=∠CBF。∴∠GAB=∠GBA。
∴GA=GB,即△GAB为等腰三角形。
由等腰梯形ABCD中,AB∥DC,DE=CF,利用SAS,易证得△ADE≌△BCF,即可得∠DAE=∠CBF,则可得∠GAB=∠GBA,然后由等角对等边,即可证得△GAB是等腰三角形。
∴∠D=∠C,∠DAB=∠CBA,
在△ADE和△BCF中,∵
 ,∴△ADE≌△BCF(SAS)。
,∴△ADE≌△BCF(SAS)。∴∠DAE=∠CBF。∴∠GAB=∠GBA。
∴GA=GB,即△GAB为等腰三角形。
由等腰梯形ABCD中,AB∥DC,DE=CF,利用SAS,易证得△ADE≌△BCF,即可得∠DAE=∠CBF,则可得∠GAB=∠GBA,然后由等角对等边,即可证得△GAB是等腰三角形。

练习册系列答案
相关题目
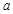 、b、c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③
、b、c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③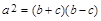 ;④
;④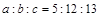 ,其中能判断△ABC是直角三角形的个数有( )
,其中能判断△ABC是直角三角形的个数有( )

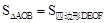 中正确的有
中正确的有