Question

【题目】综合与实践

旋转是图形变化的方法之一，借助旋转知识可以解决线段长、角的大小、取值范围、判断三角形形状等问题，在实际生活中也有着十分重要的地位和作用.

问题背景

一块等边三角形建筑材料内一点到三角形三个顶点的距离满足一定条件时，我们可以用所学的知识帮助工人师傅在没有刻度尺的情况下求出等边三角形的边长.

数学建模

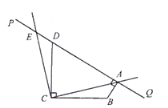
如图，等边三角形内有一点，已知，，.

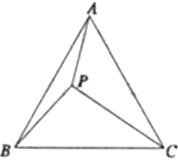
问题解决

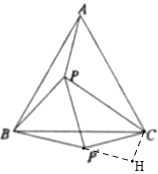
（1）如图，将△ABP绕点顺时针旋转60°得到△CBP′，连接，易证∠BP′P=__°，△____为等边三角形，____，___°.

（2）点H为直线BP′上的一个动点，则的最小值为______；

（3）求长；

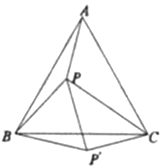
拓展延伸

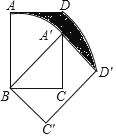
己知：点在正方形内，点在平面内，，.

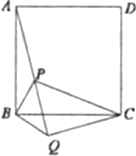
（4）在图中，连接PA、PC、PQ、QC，，若点、、在一条直线上，则____.

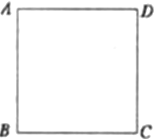
（5）若，连接，则____________；连接，当、、三点在同一条直线上时，△BDQ的面积为______.

Answer 1

【答案】（1）60°，△BP′P，∠CP′P，150；（2）；（3）；（4）；（5），，

【解析】

（1）根据旋转的性质可得BP=BP′，∠PBP′=60°，AP=P′C，∠APB=∠BP′C，即可求出∠BP′P=60°，即可得△BP′P是等边三角形，根据勾股定理的逆定理可得∠CP′P=90°，即可得∠CP′B的度数，根据旋转性质可得∠APB=∠CP′B，即可得∠APB的度数；（2）过C作CH⊥BP′，交BP′的延长线于H，根据含30°角的直角三角形的性质求出CH的值即为最小值；（3）利用勾股定理可求出HP′的长，即可得BH的长，利用勾股定理求出BC的长进而可得答案；（4）由等腰直角三角形的性质可得∠BPQ=∠BQP=45°，PQ=，根据两锐角互余的关系可得∠CBQ=∠ABP，利用SAS可证明△ABP≌△CBQ，进而可得PA=CQ，∠BQC=∠BPA=135°，可得∠PQC=90°，利用勾股定理可求出PC的长，根据余弦的定义即可得答案；（5）连接BD，以B为圆心，1为半径画圆，交BD于P，交AB、BC于E、F，连接DF，则OP为最小值，根据正方形的性质及勾股定理求出DP、DF的值即可；当D、P、Q在同一条直线上时，过B作BM⊥DQ，根据等腰直角三角形的性质可得BM=QM=PQ，利用勾股定理可求出DM的长，进而可得DQ的长，利用三角形面积公式即可得答案.

（1）∵△ABP绕点顺时针旋转60°得到△CBP′，

∴BP=BP′=4，∠PBP′=60°，AP=P′C=2，∠APB=∠BP′C，

∴∠BP′P=60°，

∴△BP′P是等边三角形，

∴PP′=BP=4，

∵PC2=(2)2=28，PP′2=42=16，P′C2=(2)2=12，

∴PC2= PP′2+ P′C2，

∴△PP′C是直角三角形，∠CP′P=90°，

∴∠BP′C=∠CP′P+∠BP′P=90°+60°=150°，

∴∠APB=∠BP′C=150°，

故答案为：60°，△BP′P，∠CP′P，150°

（2）过C作CH⊥BP′，交BP′的延长线于H，

∵∠BP′C=150°，

∴∠P′HC=180°-150°=30°，

∴CH=P′C=，

故答案为：

（3）∵CH=，P′C=PA=2，

∴P′H==3，

∴BC===2，

∴AB=BC=2.

（4）∵BP=BQ=1，BQ⊥BP，

∴∠BPQ=∠BQP=45°，PQ=，

∴∠APB=135°，

∵∠ABP+∠PBC=90°，∠CBQ+∠PBC=90°，

∴∠ABP=∠CBQ，

∵AB=BC，∠ABP=∠CBQ，BQ=BP，

∴△ABP≌△CBQ，

∴QC=AP=，∠BQC=∠APB=135°，

∴∠PQC=90°，

∴PC==，

∴cos∠PCQ===，

故答案为：

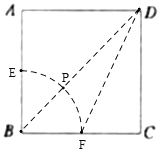
（5）如图，连接BD，以B为圆心，1为半径画圆，交BD于P，交AB、BC于E、F，连接DF，

∵BP=1，

∴点P在以B为圆心，1为半径的圆上，

∴DP为最小值，

∵AB=AD=2，

∴BD=2，

∴DP=BD-BP=2-1，

∵BF=1，CD=2，

∴DF=，

∵点P在正方形内，

∴2-1≤DP<，

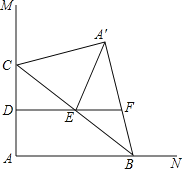
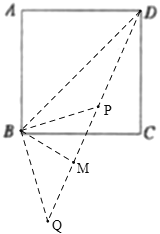
如图，当D、P、Q在同一条直线上时，过B作BM⊥DQ，

∵BQ=BP=1，BQ⊥BP，

∴BM=QM=PQ=，

∴DM==，

∴DQ=DM+QM=+=，

∴S△BDQ=××=，

故答案为：2-1，，