题目内容
 如图,已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点B的坐标为(3,-
如图,已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点B的坐标为(3,- ).
).
(1)求该抛物线的解析式及点A的坐标;
(2)在抛物线上求点P,使S△POA=2S△AOB.
解:(1)由函数图象经过原点得,函数解析式为y=ax2+bx(a≠0),
又∵函数的顶点坐标为(3,- ),
),
∴ ,
,
解得: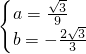 ,
,
故函数解析式为:y= x2-
x2- x,
x,
 由二次函数图象的对称性可得点A的坐标为(6,0);
由二次函数图象的对称性可得点A的坐标为(6,0);
(2)∵S△POA=2S△AOB,
∴点P到OA的距离是点B到OA距离的2倍,即点P的纵坐标为2 ,
,
代入函数解析式得:2 =
= x2-
x2- x,
x,
解得:x1=3+3 ,x2=3-3
,x2=3-3 ,
,
即满足条件的点P有两个,其坐标为:P1(3+3 ,2
,2 ),P2(3-3
),P2(3-3 ,2
,2 ).
).
分析:(1)根据函数经过原点,可得c=0,然后根据函数的对称轴,及函数图象经过点(3,- )可得出函数解析式,根据二次函数的对称性可直接得出点A的坐标.
)可得出函数解析式,根据二次函数的对称性可直接得出点A的坐标.
(2)根据题意可得点P到OA的距离是点B到OA距离的2倍,即点P的纵坐标为2 ,代入函数解析式可得出点P的横坐标.
,代入函数解析式可得出点P的横坐标.
点评:此题考查了二次函数的综合题目,涉及了待定系数法求函数解析式,三角形的面积及一元二次方程的解,综合性较强,需要我们仔细分析,分步解答.
又∵函数的顶点坐标为(3,-
 ),
),∴
 ,
,解得:
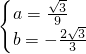 ,
,故函数解析式为:y=
 x2-
x2- x,
x, 由二次函数图象的对称性可得点A的坐标为(6,0);
由二次函数图象的对称性可得点A的坐标为(6,0);(2)∵S△POA=2S△AOB,
∴点P到OA的距离是点B到OA距离的2倍,即点P的纵坐标为2
 ,
,代入函数解析式得:2
 =
= x2-
x2- x,
x,解得:x1=3+3
 ,x2=3-3
,x2=3-3 ,
,即满足条件的点P有两个,其坐标为:P1(3+3
 ,2
,2 ),P2(3-3
),P2(3-3 ,2
,2 ).
).分析:(1)根据函数经过原点,可得c=0,然后根据函数的对称轴,及函数图象经过点(3,-
 )可得出函数解析式,根据二次函数的对称性可直接得出点A的坐标.
)可得出函数解析式,根据二次函数的对称性可直接得出点A的坐标.(2)根据题意可得点P到OA的距离是点B到OA距离的2倍,即点P的纵坐标为2
 ,代入函数解析式可得出点P的横坐标.
,代入函数解析式可得出点P的横坐标.点评:此题考查了二次函数的综合题目,涉及了待定系数法求函数解析式,三角形的面积及一元二次方程的解,综合性较强,需要我们仔细分析,分步解答.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;