题目内容
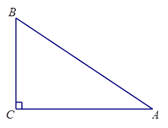
【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C出发,沿线段CA向点A运动,到达A点后停止运动,且速度为每秒2cm,设出发的时间为t秒.
(1)当t为何值时,△PBC是等腰三角形;
(2)过点P作PH⊥AB,垂足为H,当H为AB中点时,求t的值.
【答案】(1)3;(2)![]()
【解析】试题分析: ![]() 当
当![]() 为等腰三角形时,则可知其为等腰直角三角形,则有
为等腰三角形时,则可知其为等腰直角三角形,则有![]() ,可求得
,可求得![]() 的值;
的值;![]() 由题意可知
由题意可知![]() 为线段
为线段![]() 的垂直平分线,则有PB=PA,可用
的垂直平分线,则有PB=PA,可用![]() 表示出PA和PB的长,在
表示出PA和PB的长,在![]() 中由勾股定理可列方程,可求得
中由勾股定理可列方程,可求得![]() 的值.
的值.
试题解析: ![]()
∴当![]() 为等腰三角形时,其必为等腰直角三角形,
为等腰三角形时,其必为等腰直角三角形,
![]()
由题意可知![]() 且
且![]()
![]()
解得![]()
即当![]() 为
为![]() 秒时,
秒时, ![]() 为等腰三角形;
为等腰三角形;
![]() 如图:
如图:
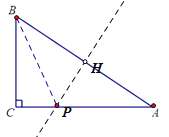
在![]() 中,
中, ![]()
![]()
![]() 且H为AB中点,
且H为AB中点,
∴PH垂直平分AB,
∴PB=PA,
由题意可知![]()
则![]()
在![]() 中,由勾股定理可得
中,由勾股定理可得![]()
即![]() 解得
解得![]()
即当H为AB中点时,t的值为![]() .
.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目