Question

【题目】如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．∠BAD=60°，AC平分∠BAD，AC=2，BN的长为 ．

Answer 1

【答案】
【解析】解：在△CAD中，∵M、N分别是AC、CD的中点，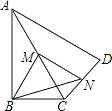

∴MN∥AD，MN= AD，

在Rt△ABC中，∵M是AC中点，

∴BM= AC，

∵AC=AD，

∴MN=BM，

∵∠BAD=60°，AC平分∠BAD，

∴∠BAC=∠DAC=30°，

∴BM= AC=AM=MC，

∴∠BMC=∠BAM+∠ABM=2∠BAM=60°，

∵MN∥AD，

∴∠NMC=∠DAC=30°，

∴∠BMN=∠BMC+∠NMC=90°，

∴BN2=BM2+MN2，

∴MN=BM= AC=1，

∴BN= ．

所以答案是： ．

【考点精析】关于本题考查的直角三角形斜边上的中线和勾股定理的概念，需要了解直角三角形斜边上的中线等于斜边的一半；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．