题目内容
已知:如下图,在平面直角坐标系中,点M在x轴的负半轴上,以M为圆心画半圆,交x轴于A,B两点,交y轴的正半轴于C,过C作半圆M的切线CP,交x轴于P,若AO∶OB=4∶1,PC+PA=12cm,
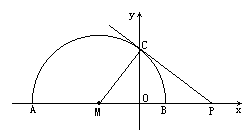
(1)求OC的长;
(2)在y轴的负半轴上是否存在点E,使以A,O,E为顶点的三角形与△POC相似,如果存在,求图像经过A,E两点的一次函数解析式;若不存在,说明理由.
答案:
解析:
解析:
|
解:(1)连结AC、BC,因为AB为直径, 所以AC⊥BC,又CO⊥AB,△AOC∽△ACB, 所以 同理可证 因为PC切圆M于C,所以∠BAC=∠PCB,又∠APC为公共角,所以△PAC∽△PCB, 由已知,PC+PA=12cm,所以PC+2PC=12cm,3PC=12cm,PC=4cm,PA=8cm. 由切割线定理,有 因为AO∶OB=4∶1,所以OB=
(2)设点E存在,若 所以 则有 所以所求一次函数解析式为 这时点 所以符合条件的点E存在,有两个,所求一次函数解析式为y=-
|

练习册系列答案
相关题目
 =AO·AB,
=AO·AB, =BO·AB,
=BO·AB,
 ,即PA=2PC,
,即PA=2PC, =PB·8,PB=2cm,AB=PA-PB=8-2=6cm.
=PB·8,PB=2cm,AB=PA-PB=8-2=6cm. cm,AO=
cm,AO= cm,又
cm,又 =AO·OB,所以OC=
=AO·OB,所以OC= cm.
cm.
 ∽△POC,
∽△POC,
 =
= cm,即点
cm,即点 (0,-
(0,- ),点A(-
),点A(- ,0),设直线
,0),设直线 的解析式为y=kx+b,
的解析式为y=kx+b,


 (0,-
(0,- ),可求得
),可求得 的解析式为y
的解析式为y
 x-
x- 或y=-
或y=-

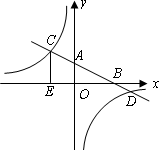


 的图像与反比例函数
的图像与反比例函数 的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2),
的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2), ,则此一次函数的解析式为 .
,则此一次函数的解析式为 .