题目内容
已知:△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E、F分别是线段BC
和线段BD上的点,且点F在线段EC的垂直平分线上,连接AF、AE,AE交BD于点G.
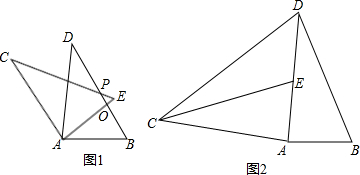
(1)如图l,求证:∠EAF=∠ABD;
(2)如图2,当AB=AD时,M是线段AG上一点,连接BM、ED、MF,MF的延长线交ED于点N,∠MBF=![]() ∠BAF,AF=
∠BAF,AF=![]() AD,试探究线段FM和FN之间的数量关系,并证明你的结论.
AD,试探究线段FM和FN之间的数量关系,并证明你的结论.

考点:本题考查了三角形全等的判断和性质,相似三角形的判断和性质,平行线分线段成比例定理,轴对称性质,三角形四边形内角和,线段的垂直平分线性质
要求较高的视图能力和证明推理能力。
分析:(1)连接FE、FC,先证△ABF、△CBF全等,得∠FEC=∠BAF,通过四边形ABEF与三角形AEF内角和导出;(2)先由△AFG∽△BFA,推出∠AGF=∠BAF,再得BG=MG,通过△AGF∽△DGA,导出GD=![]() a,FD=
a,FD=![]() a,过点F作FQ∥ED交AE于Q,通过BE∥AD德线段成比例设EG=2kBG=MG=3k,GQ=
a,过点F作FQ∥ED交AE于Q,通过BE∥AD德线段成比例设EG=2kBG=MG=3k,GQ=![]() EG=
EG=![]() ,MQ=3k+
,MQ=3k+![]() =
=![]() ,从而FM=
,从而FM=![]() FN本题综合考查了相似三角形线段之间的比例关系、平行线分线段成比例定理等重要知识点,难度较大.在解题过程
FN本题综合考查了相似三角形线段之间的比例关系、平行线分线段成比例定理等重要知识点,难度较大.在解题过程![]() 中,涉及到数目较多的线段比,注意不要出错
中,涉及到数目较多的线段比,注意不要出错
解答:(1)证明:如图1 连接FE、FC ∵点F在线段EC的垂直平分线上
∴.FE=FC ∴∠l=∠2 ∵△ABD和△CBD关于直线BD对称.∴AB=CB ∠4=∠3 BF=BF
∴△ABF≌ACBF ∴∠BAF=∠2 FA=FC ∴FE=FA ∠1=∠BAF. ∴∠5=∠6 ∵ ∠l+∠BEF=1800∠BAF+∠BEF=1800
∵∠BAF+∠BEF+∠AFE+∠ABE=3600 ∴.∠AFE+∠ABE=1800 又∵∠AFE+∠5+∠6=1800 ∴∠5+∠6=∠3+∠4 ∴∠5=∠4
即∠EAF=∠ABD
(2)FM=![]() FN 证明:如图2 由(1)可知∠EAF=∠ABD
FN 证明:如图2 由(1)可知∠EAF=∠ABD
又∵∠AFB=∠GFA ∴△AFG∽△BFA
∴∠AGF=∠BAF
又∵∠MBF=![]() ∠BAF.∠MBF=
∠BAF.∠MBF=![]() ∠AGF
∠AGF
又∵∠AGF=∠MBG+∠BMG
∴∠MBG=∠BMG ∴BG=MG
∵AB=AD ∴∠ADB=∠ABD=∠EAF
又∵∠FGA=∠AGD.∴△AGF∽△DGA.![]() ∵AF=
∵AF=![]() AD
AD![]()
设GF=2a AG=3a.∴GD=![]() a
a
∴FD==![]() a∵∠CBD=∠ABD ∠ABD=∠ADB
a∵∠CBD=∠ABD ∠ABD=∠ADB
∴.∠CBD=∠ADB∴BE//AD.∴![]()
![]()
设EG=2k∴BG=MG=3k 过点F作FQ∥ED交AE于Q
 ∴
∴![]()
∴GQ=![]() EG=
EG=![]() . MQ=3k+
. MQ=3k+![]() =
=![]()
∵FQ∥ED![]() ∴FM=
∴FM=![]() FN
FN



 名校课堂系列答案
名校课堂系列答案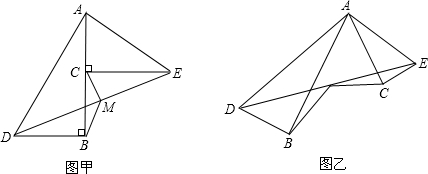

 ,
, ,
,
 ≌
≌ ;
; ,
, ,
, ,
, 的度数
的度数 度(
度( ),问当
),问当 ,连接CD,若
,连接CD,若 的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。
的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。

 ∠BAF,AF=
∠BAF,AF=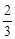 AD,试探究线段FM和FN之间的数量关系,并证明你的结论.
AD,试探究线段FM和FN之间的数量关系,并证明你的结论.