题目内容
 如图,把边长是3的正方形等分成9个小正方形,在有阴影的两个小正方形内(包括边界)分别取点P、R,与已有格点Q(每个小正方形的顶点叫格点)构成三角形,则△PQR的最大面积是________.
如图,把边长是3的正方形等分成9个小正方形,在有阴影的两个小正方形内(包括边界)分别取点P、R,与已有格点Q(每个小正方形的顶点叫格点)构成三角形,则△PQR的最大面积是________.
2
分析:本题需先根据题意找出点p、Q、R的位置,然后再根据三角形面积公式即可求出结果.
解答: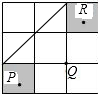 解:当点P、Q、R构成如图所示的三角形时,所围成的三角形的面积最大
解:当点P、Q、R构成如图所示的三角形时,所围成的三角形的面积最大
S△PQR=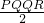
=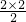
=2
∴△PQR的最大面积是2
故答案为2.
点评:本题主要考查了正方形的性质,解题时要确定出P、R的位置是解题的关键.
分析:本题需先根据题意找出点p、Q、R的位置,然后再根据三角形面积公式即可求出结果.
解答:
 解:当点P、Q、R构成如图所示的三角形时,所围成的三角形的面积最大
解:当点P、Q、R构成如图所示的三角形时,所围成的三角形的面积最大S△PQR=
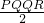
=
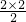
=2
∴△PQR的最大面积是2
故答案为2.
点评:本题主要考查了正方形的性质,解题时要确定出P、R的位置是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
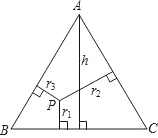






 AB•r1+
AB•r1+

 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).
