��Ŀ����
����Ŀ����֪![]() ����С������������
����������������![]() ����
����![]() ����ش�
����ش�
��1����ֱ��д��![]() ��ֵ��
��ֵ��![]() ��______��
��______��![]() =______��
=______��![]() ��______��
��______��
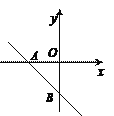
��2���ڣ�1���������£�����PΪһ���㣬���Ӧ����Ϊ![]() ����P��0��2֮���˶�����
����P��0��2֮���˶�����![]() ʱ������
ʱ������![]() ��
��
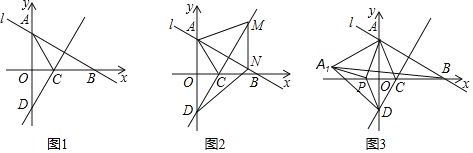
��3���ڣ�1����2���������£�![]() ��b��c�ֱ��Ӧ�ĵ�A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶�������
��b��c�ֱ��Ӧ�ĵ�A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶�������![]() ���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB�����ʣ�BC��AB��ֵ�Ƿ�����ʱ��
���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB�����ʣ�BC��AB��ֵ�Ƿ�����ʱ��![]() �ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
![]()
���𰸡���1����1��1��5����2����x+6��3x+8����3�����䣬BC��AB=2.
��������
��1������b����С��������������ȷ��b��ֵ��Ȼ����ݷǸ��������ʣ������Ǹ����ĺ���0����ÿ������0���������a��b��c��ֵ��
��2�����������������x��ȡֵ��Χ��ȷ��x+1��x-1��x-2�ķ��ţ�Ȼ����ݾ���ֵ�����廯�ɣ�
��3���Ȱ�AB��BC�ú�t��ʽʾ�������ٵõ�BC-AB=2���Ӷ��ó�BC-AB��ֵΪ��ֵ��
�⣺��1��������ã�b��1��c��5��0��a+b��0
���a����1�� b��1�� c��5��
�ʴ�Ϊ����1��1��5��
��2������P��0��2֮���˶�ʱ��0��x��2��
��ˣ�������������ۣ�
�ٵ�0��x��1ʱ��x+1��0��x��1��0��x��2��0��
ԭʽ��x+1��1+x+6��3x����x+6��
�ڵ�1��x��2ʱ��x+1��0��x��1��0��x��2��0��
ԭʽ��x+1��x+1+6��3x����3x+8��
���ϣ�����![]() �Ľ��Ϊ��x+6��3x+8��
�Ľ��Ϊ��x+6��3x+8��
��3�����ۣ����䣬BC��AB=2��
���ɣ�
����t�룬��A�����˶���t����λ���ȣ���B�����˶���2t����λ���ȣ���C�����˶���5t����λ���ȣ�����ʼ�˶�֮ǰ��AB=1-(-1)=2��BC=5-1=4,
���˶�t���AB=t+2t+2=3t+2��BC=5t-2t+4=3t+4��
��AB��3t+2��BC��3t+4
��BC��AB����3t+4��-(3t+2)=2
��BC��AB��ֵ���䣬BC��AB=2��