题目内容
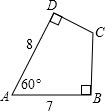四边形ABCD，∠B=∠D=90°，∠A=60°，AD=8，AB=7，则BC+CD=________．
分析：作出辅助线，延长BC、AD交于E点，根据直角三角形的特殊性，以及在直角三角形中30°所对的边是斜边的一半，分别得出DE，EC，BC的长，从而求出．
解答：延长BC、AD交于E点，
则 Rt△EBA的，∠E=30°，AB=7，
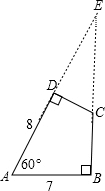
∴AE=2AB=14，
∴DE=6
同理 Rt△EDC的，∠E=30°，
∴EC=2DC，代入DC2+DE2=EC2，
得DC=2
，EC=4，同理Rt△EAB中用勾股定理得BE=7
，所以BC=3
BC+CD=5．故答案为：5
．点评：此题主要考查了勾股定理的应用以及三角函数的应用，此题综合性较强，也是中考中热点问题，遇到类似图形作出延长两边的辅助线较多，应注意学会应用这种辅助线的作法．
练习册系列答案
相关题目
12、如图所示，在四边形ABCD中，AD∥BC，BC＞AD，∠B与∠C互余，将AB，CD分别平移到EF和EG的位置，则△EFG为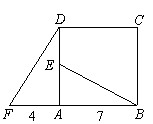
18、四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如图所示，如果AF=4，AB=7，
22、如图所示，在平行四边形ABCD中，AE⊥BD，FC⊥BD，垂足分别为E，F．