Question

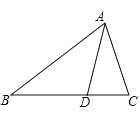
【题目】将一副三角板按如图方法摆放在一起，连接AC，则tan∠DAC值为（ ）

A.1

B.

C.

D.

Answer 1

【答案】C

【解析】

试题分析：先过点C作CE⊥AD于E，设CD=a，在Rt△BDC中，利用三角函数，可求BD，在Rt△DBA中，利用三角函数，可求AD，易证△CED是等腰直角三角形，从而利用三角函数可求CE、DE，于是在Rt△CAE中，可求tan∠EAC==，即tan∠DAC的值.

解：如图所示，过点C作CE⊥AD于E，

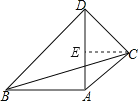
设CD=a，

在Rt△BDC中，∠DBC=30°，则

BD=cot30°×CD=a，

在Rt△DBA中，AD=sin45°×BD=a，

又∵CE⊥AD，∠BDA=45°，

∴DE=CE=sin45°×a=a，

∴在Rt△CAE中，tan∠EAC====.

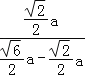即tan∠DAC=.

故选：C.