题目内容
17、如图，P为?ABCD的对角线BD上一点，过P作GH∥CD，EF∥BC，写出图中你认为面积相等的平行四边形有S?ABHG=S?BCFE，S?AGPE=S?HCFP，S?AEFD=S?HCDG
．分析：根据平行四边形的性质证全等三角形，然后利用等量关系推出面积相等．
解答：解：∵?ABCD
∴S△ABD=S△CBD．
∵BP是平行四边形BEPH的对角线，
∴S△BEP=S△BHP，
∵PD是平行四边形GPFD的对角线，
∴S△GPD=S△FPD．S△ABD-S△GPD=S△BCD-S△PFD．即S?ABHG=S?BCFE，
同理S?AGPE=S?HCFP，S?AEFD=S?HCDG．即：S?ABHG=S?BCFE，S?AGPE=S?HCFP，S?AEFD=S?HCDG．
故答案为S?ABHG=S?BCFE，S?AGPE=S?HCFP，S?AEFD=S?HCDG．
∴S△ABD=S△CBD．
∵BP是平行四边形BEPH的对角线，
∴S△BEP=S△BHP，
∵PD是平行四边形GPFD的对角线，
∴S△GPD=S△FPD．S△ABD-S△GPD=S△BCD-S△PFD．即S?ABHG=S?BCFE，
同理S?AGPE=S?HCFP，S?AEFD=S?HCDG．即：S?ABHG=S?BCFE，S?AGPE=S?HCFP，S?AEFD=S?HCDG．
故答案为S?ABHG=S?BCFE，S?AGPE=S?HCFP，S?AEFD=S?HCDG．
点评：本题考查的是平行四变形的性质，平行四边形的一条对角线可以把平行四边形分成两个全等的三角形，两条对角线把平行四边形的面积一分为四，同时充分利用等量相加减原理解题．
练习册系列答案
相关题目
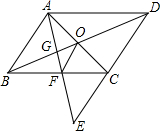已知：如图，E为?ABCD中DC边的延长线上一点，且CE=DC，连接AE，分别交BC、BD于点F、G，连接AC交BD于O，连接OF，判断AB与OF的位置关系和大小关系，并证明你的结论．
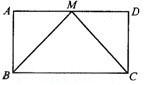34、已知：如图，M为?ABCD的AD边上的中点，且MB=MC，
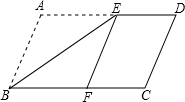如图，E为?ABCD中AD边上的一点，将△ABE沿BE折叠使得点A刚好落在BC边上的F点处，若AB为4，ED为3，则?ABCD的周长为
如图，E为?ABCD的边BC延长线上一点，AE与BD交于点F，与DC交于点G．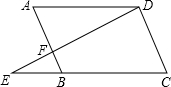
如图，E为?ABCD的边CB的延长线上一点，DE交AB于点F，则图中与△ADF相似的三角形是