Question

如图，△ABC的面积为3，∠B=15°，点D在边BC上，DA⊥AB．设BC=x，BD=y．则y关于x的函数解析式为________，定义域为________．

Answer 1

    
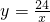
分析：首先过点A作AH⊥BD于点H，根据△ABC的面积是3表示出AH，再利用BD及15°的正弦值与余弦值表示出AH，然后整理求解即可得到y与x之间的函数解析式；又由点D在边BC上，可得x≥y，继而求得定义域．
解答：解：过点A作AH⊥BD于点H，
则S_△ABC=BC•AH=3，
∵BC=x，
∴AH=，
又∵AH=ABsin15°=BDcos15°•sin15°，
∴AH=ycos15°•sin15°，
即：=ycos15°•sin15°=y××，
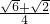∴y=．
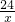由点D在边BC上，
∴x≥y，
即x≥，
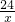∵x＞0，
∴x²≥24，
即x≥2，
∴定义域为x≥2．
故答案为：y=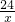，x≥2．
点评：此题考查了三角形面积的求解方法与三角函数的知识．此题难度适中，解题的关键是准确作出辅助线，掌握三角形面积的求解方法．