题目内容
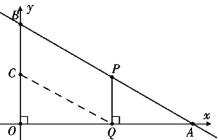
【题目】如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1 , AA2 , AA3…,依此作法,则∠AAnAn+1等于度.(用含n的代数式表示,n为正整数) 
【答案】(180﹣ ![]() )
)
【解析】解:∵点A绕点O顺时针旋转后的对应点A1落在射线OB上,
∴OA=OA1 ,
∴∠AA1O= ![]() ,
,
∵点A绕点A1顺时针旋转后的对应点A2落在射线OB上,
∴A1A=A1A2 ,
∴∠AA2A1= ![]() ∠AA1O=
∠AA1O= ![]() ,
,
∵点A绕点A2顺时针旋转后的对应点A3落在射线OB上,
∴A2A=A2A3 ,
∴∠AA3A2= ![]() ∠AA2A1=
∠AA2A1= ![]() ,
,
∴∠AAnAn﹣1= ![]() ,
,
∴∠AAnAn+1=180°﹣ ![]() .
.
故答案为:180﹣ ![]() .
.
根据旋转的性质得OA=OA1 , 则根据等腰三角形的性质得∠AA1O= ![]() ,同理得到A1A=A1A2 , 根据等腰三角形的性质和三角形外角性质得到∠AA2A1=
,同理得到A1A=A1A2 , 根据等腰三角形的性质和三角形外角性质得到∠AA2A1= ![]() ∠AA1O=
∠AA1O= ![]() ,同样得到∠AA3A2=
,同样得到∠AA3A2= ![]() ,于是可推广得到∠AAnAn﹣1=
,于是可推广得到∠AAnAn﹣1= ![]() ,然后利用邻补角的定义得到∠AAnAn+1=180°﹣
,然后利用邻补角的定义得到∠AAnAn+1=180°﹣ ![]() .
.

练习册系列答案
相关题目