题目内容
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
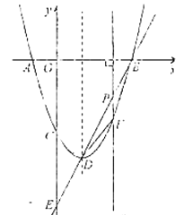
(Ⅰ)求顶点![]() 的坐标;
的坐标;
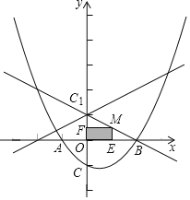
(Ⅱ)如图,设点![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点![]() .求
.求![]() 的面积最大值;
的面积最大值;
(Ⅲ)点![]() 在线段
在线段![]() 上,当
上,当![]() 时,求点
时,求点![]() 的坐标(直接写出结果,不必写解答过程).
的坐标(直接写出结果,不必写解答过程).
【答案】(Ⅰ)(1,-4);(Ⅱ)1;(Ⅲ)(![]() ,-
,-![]() )
)
【解析】
(Ⅰ)利用待定系数法把![]() ,
,![]() ,代入二次函数
,代入二次函数![]() 中,即可算出b、c的值,得到函数解析式,再用配方法求得顶点
中,即可算出b、c的值,得到函数解析式,再用配方法求得顶点![]() 的坐标;
的坐标;
(Ⅱ)先根据B、D两点坐标利用待定系数法确定直线BD的解析式,设点P的坐标为(m,n),再根据![]() ,得出
,得出![]() 关于点P的横坐标m的函数关系式,利用配方法即可得出结论;
关于点P的横坐标m的函数关系式,利用配方法即可得出结论;
(Ⅲ)根据B、C、D三点的坐标,利用两点间的距离公式分别求出CD、BD、CB的平方,再利用勾股定理的逆定理确定![]() BCD为直角三角形,求出tan∠CDB的值,设点Q的坐标为(n,2n-6),再根据已知条件得出tan∠QCE=3,从而列出n的方程,解方程即可确定Q点坐标.
BCD为直角三角形,求出tan∠CDB的值,设点Q的坐标为(n,2n-6),再根据已知条件得出tan∠QCE=3,从而列出n的方程,解方程即可确定Q点坐标.
(Ⅰ)∵抛物线y=x2-bx+c的图象经过点A(-1,0),B(3,0),
∴![]() ;
;
解得:![]()
∴抛物线的解析式为y=x2-2x-3=(x-1)2-4;
∴顶点![]() 的坐标为:(1,-4);
的坐标为:(1,-4);
(Ⅱ)设直线BD解析式为y=kx+b,
∵![]() ,D(1,-4).
,D(1,-4).
∴![]() ;
;
解得:![]()
∴直线BD解析式为y=2x-6,
设点P的坐标为(m,n),
∵点![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),
重合),
∴点P的坐标为:(m,2m-6)(1![]() );
);
∵点![]() 是过点
是过点![]() 作
作![]() 轴的垂线与抛物线的交点.
轴的垂线与抛物线的交点.
∴点F的坐标为:(m,m2-2m-3);
∵点P在点F的上方,
∴PF=(2m-6)-(m2-2m-3)=-m2+4m-3
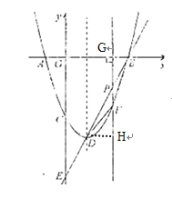
设直线PF交x轴于点G,过点D作DH⊥PF于H,
∵![]()
=-m2+4m-3=-![]() .
.
∴![]() 是关于m的二次函数;
是关于m的二次函数;
∵a=-1![]() ,
,
∴当m=2时,![]() 的面积有最大值,最大值为1.
的面积有最大值,最大值为1.
(Ⅲ)点Q的坐标为(![]() ,-
,-![]() )
)
连接BC、CD,由点![]() 、
、![]() 、
、![]() (1,-4);
(1,-4);
根据两点间的距离公式可得:![]() ,
,![]() ,
,
![]() ;
;
∴![]()
∴∠DCB=90°
在Rt![]() 中,tan∠CDB=
中,tan∠CDB=![]()
∵∠CDB=∠QCE,∴tan∠QCE =3,
设点Q的坐标为(n,2n-6)
过点Q作QM⊥CE于M,
在Rt![]() 中,tan∠QCE=
中,tan∠QCE=![]() =3,∴n=
=3,∴n=![]()
∴点Q的坐标为(![]() ,-
,-![]() )
)