题目内容
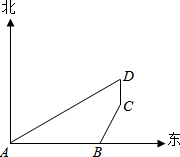 南海某舰艇在A处执行巡逻任务,在其正东方向8海里处有一小岛B,在B的北偏东30°方向上有一小岛C,在小岛C的正北方向2海里处有一岛D,测得小岛D在A的北偏东60°向上,求小岛B与C之间的距离(结果保留根号)
南海某舰艇在A处执行巡逻任务,在其正东方向8海里处有一小岛B,在B的北偏东30°方向上有一小岛C,在小岛C的正北方向2海里处有一岛D,测得小岛D在A的北偏东60°向上,求小岛B与C之间的距离(结果保留根号)
解:延长DC交AU延长线于点E,
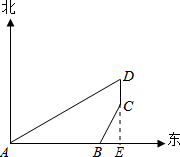
由题意得,∠CBE=60°,∠DAE=30°,
设BC=x,
在Rt△BCE中,BE= BC=
BC= x,CE=
x,CE= x,
x,
则AE=AB+BE=8+ x,DE=CD+CE=2+
x,DE=CD+CE=2+ x,
x,
在Rt△ADE中,tan∠DAE= =
=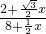 =
= ,
,
解得:x= .
.
答:小岛B与C之间的距离为 海里.
海里.
分析:延长DC交AU延长线于点E,设BC=x,在Rt△BCE中表示出BE、CE,继而可表示出AE、DE,在Rt△ADE中,根据tan∠DAE的值,可解出x.
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,明白方向角的定义,利用三角函数表示相关线段的长度.

由题意得,∠CBE=60°,∠DAE=30°,
设BC=x,
在Rt△BCE中,BE=
 BC=
BC= x,CE=
x,CE= x,
x,则AE=AB+BE=8+
 x,DE=CD+CE=2+
x,DE=CD+CE=2+ x,
x,在Rt△ADE中,tan∠DAE=
 =
=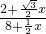 =
= ,
,解得:x=
 .
.答:小岛B与C之间的距离为
 海里.
海里.分析:延长DC交AU延长线于点E,设BC=x,在Rt△BCE中表示出BE、CE,继而可表示出AE、DE,在Rt△ADE中,根据tan∠DAE的值,可解出x.
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,明白方向角的定义,利用三角函数表示相关线段的长度.

练习册系列答案
相关题目
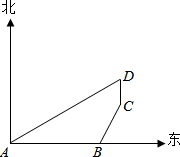 (2013•凤阳县模拟)南海某舰艇在A处执行巡逻任务,在其正东方向8海里处有一小岛B,在B的北偏东30°方向上有一小岛C,在小岛C的正北方向2海里处有一岛D,测得小岛D在A的北偏东60°向上,求小岛B与C之间的距离(结果保留根号)
(2013•凤阳县模拟)南海某舰艇在A处执行巡逻任务,在其正东方向8海里处有一小岛B,在B的北偏东30°方向上有一小岛C,在小岛C的正北方向2海里处有一岛D,测得小岛D在A的北偏东60°向上,求小岛B与C之间的距离(结果保留根号)