题目内容
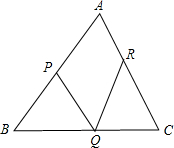 如图,点P,Q,R分别在△ABC的边上AB、BC、CA上,且BP=PQ=QR=RC=1,那么,△ABC面积的最大值是
如图,点P,Q,R分别在△ABC的边上AB、BC、CA上,且BP=PQ=QR=RC=1,那么,△ABC面积的最大值是
- A.

- B.2
- C.

- D.3
B
分析:首先,若以Ⅰ,Ⅱ,Ⅲ,Ⅳ分别记△APR,△BPQ,△CRQ,△PQR,利用三角形内角和定理,求证:h2≤h1(h1,h2分别为△QRP,△APR公共边PR上的高.因若作出△PQR关于PR的对称图形PQ′R,这时Q′,A都在以PR为弦的含∠A的弓形弧上,且因PQ′=Q′R,所以Q′为这弧中点,故可得出h2≤h1).最后,当AB=AC-2,∠A=90°时,即可得出△ABC面积的最大值.
解答: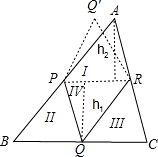 解:首先,若以Ⅰ,Ⅱ,Ⅲ,Ⅳ分别记△APR,△BPQ,△CRQ,△PQR,
解:首先,若以Ⅰ,Ⅱ,Ⅲ,Ⅳ分别记△APR,△BPQ,△CRQ,△PQR,
则SⅡ,SⅢ,SⅣ均不大于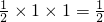 .
.
又∵∠PQR=180°-(∠B+∠C)=∠A,
∴h2≤h1(h1,h2分别为△QRP,△APR公共边PR上的高,因若作出△PQR关于PR的对称图形PQ′R,这时Q′,A都在以PR为弦的含∠A的弓形弧上,且因PQ′=Q′R,所以Q′为这弧中点,故可得出h2≤h1).
从而S1≤SⅣ≤ ,这样S△ABC=SⅠ+SⅡ+SⅢ+SN≤
,这样S△ABC=SⅠ+SⅡ+SⅢ+SN≤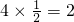
最后,当AB=AC-2,∠A=90°时,
S△ABC=2即可以达到最大值2.
故选B.
点评:此题主要考查学生对三角形面积的理解和掌握,但此题涉及的知识点较多,尤其是涉及到弧、弦、对称图形,是一道难题.
分析:首先,若以Ⅰ,Ⅱ,Ⅲ,Ⅳ分别记△APR,△BPQ,△CRQ,△PQR,利用三角形内角和定理,求证:h2≤h1(h1,h2分别为△QRP,△APR公共边PR上的高.因若作出△PQR关于PR的对称图形PQ′R,这时Q′,A都在以PR为弦的含∠A的弓形弧上,且因PQ′=Q′R,所以Q′为这弧中点,故可得出h2≤h1).最后,当AB=AC-2,∠A=90°时,即可得出△ABC面积的最大值.
解答:
 解:首先,若以Ⅰ,Ⅱ,Ⅲ,Ⅳ分别记△APR,△BPQ,△CRQ,△PQR,
解:首先,若以Ⅰ,Ⅱ,Ⅲ,Ⅳ分别记△APR,△BPQ,△CRQ,△PQR,则SⅡ,SⅢ,SⅣ均不大于
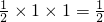 .
.又∵∠PQR=180°-(∠B+∠C)=∠A,
∴h2≤h1(h1,h2分别为△QRP,△APR公共边PR上的高,因若作出△PQR关于PR的对称图形PQ′R,这时Q′,A都在以PR为弦的含∠A的弓形弧上,且因PQ′=Q′R,所以Q′为这弧中点,故可得出h2≤h1).
从而S1≤SⅣ≤
 ,这样S△ABC=SⅠ+SⅡ+SⅢ+SN≤
,这样S△ABC=SⅠ+SⅡ+SⅢ+SN≤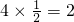
最后,当AB=AC-2,∠A=90°时,
S△ABC=2即可以达到最大值2.
故选B.
点评:此题主要考查学生对三角形面积的理解和掌握,但此题涉及的知识点较多,尤其是涉及到弧、弦、对称图形,是一道难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、EF与AD互相平分 | ||
B、EF=
| ||
| C、AD平分∠BAC | ||
| D、△DEF∽△ACB |
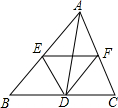 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、AD平分∠BAC | ||
B、EF=
| ||
| C、EF与AD互相平分 | ||
| D、△DFE是△ABC的位似图形 |
 5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件:
5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件: 如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是
如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是 如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )
如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )