Question

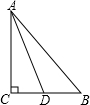
如图，△ABC中，AB=AC，BD平分∠ABC，∠BDC=72°．求∠A的度数，并指出图中所有的等腰三角形．

Answer 1

设∠A=x°
∵AB=AC，
∴∠ABC=∠C=

1

2

（180°-x°）=90°-

1

2

x°，
∵BD平分∠ABC，
∴∠ABD=∠DBC=

1

2

∠ABC=45°-

1

4

x°，
在△DBC中，∠C+∠DBC+∠BDC=180°，
∴90°-

1

2

x°+72°+45°-

1

4

x°，
解得：x=36，
即∠A=36°，
图中等腰三角形有△ABC、△BDC、△ABD．