题目内容
【题目】已知抛物线y=﹣x2+bx+c与x轴交于点A（1，0），B（3，0），与y轴交于点C．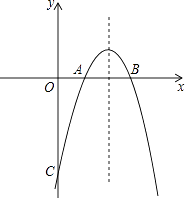 
（1）求抛物线的解析式；
（2）设点P在该抛物线上滑动，则满足S△PAB=1的点P有几个？求出所有点P的坐标；
（3）在该抛物线的对称轴上存在点M，使得△MAC的周长最小，求出这个点M的坐标．
【答案】
（1）解：将点A（1，0）、B（3，0）代入y=﹣x2+bx+c中，
得： 
，解得： 
，
∴该抛物线的解析式为y=﹣x2+4x﹣3
（2）解：设点P的坐标为（x，y）．
∵AB=2，S△PAB= 
AB|y|=1，
∴y=±1．
当y=1时，有1=﹣x2+4x﹣3，即x2﹣4x+4=（x﹣2）2=0，
解得：x1=x2=2；
当y=﹣1时，有﹣1=﹣x2+4x﹣3，即x2﹣4x+2=0，
解得：x3=2﹣ 
，x4=2+ ．
∴满足条件的点P有三个坐标分别为（2，1），（2+ ，﹣1），（2﹣ ，﹣1）
（3）解：假设存在．
过点C作抛物线的对称轴的对称点C′，连接AC′交抛物线对称轴于点M，连接MC，任取抛物线对称轴上除M外的任意一点N，连接NA，NC、NC′，如图所示．
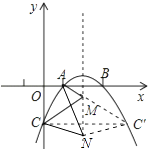
∵NA+NC=NA+NC′＞AC′=MA+MC′=MA+MC，
∴当点A、M、C′三点共线时，△MAC的周长最小．
∵抛物线的解析式为y=﹣x2+4x﹣3，
∴点C的坐标为（0，﹣3），抛物线的对称轴为x=﹣ 
=2，
∴C′（4，﹣3）．
设直线AC′的解析式为y=mx+n，
∵点A（1，0）、C′（4，﹣3）在直线AC′上，
∴ 
，解得： 
，
∴直线AC′的解析式为y=﹣x+1．
联立直线AC′的解析式和抛物线的对称轴成方程组： 
，
解得： 
．
∴直线AC′与对称轴x=2的交点为（2，﹣1），即M（2，﹣1），
∴存在点M（2，﹣1），可使△AMC的周长最小
【解析】（1）结合点A、B的坐标，利用待定系数法即可求出抛物线的解析式；（2）设点P的坐标为（x，y）．结合三角形的面积公式求出y=±1，将其代入抛物线解析式中求出x值，由此即可得出结论；（3）假设存在，过点C作抛物线的对称轴的对称点C′，连接AC′交抛物线对称轴于点M，连接MC，任取抛物线对称轴上除M外的任意一点N，连接NA，NC、NC′，利用三角形两边之和大于第三边得出点A、M、C′三点共线时，△MAC的周长最小．由抛物线的解析式找出点C的坐标以及抛物线的对称轴，利用对称的性质找出点C′的坐标，结合点A、C′的坐标利用待定系数法求出直线AC′的解析式，再联立直线AC′的解析式与抛物线的对称轴成方程组，解方程组即可求出点M的坐标．
【考点精析】根据题目的已知条件，利用抛物线与坐标轴的交点的相关知识可以得到问题的答案，需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．
