��Ŀ����
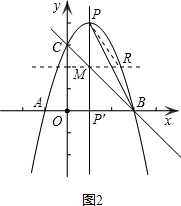
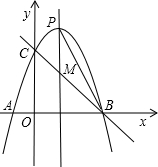 ��ͼ��������y=ax2+bx+3��x�ύ��A��-1��0����B ��3��0�����㣬��y�ύ�ڵ�C���������ߵĶԳ������������ཻ�ڵ�P����ֱ��BC�ཻ�ڵ�M������PB��
��ͼ��������y=ax2+bx+3��x�ύ��A��-1��0����B ��3��0�����㣬��y�ύ�ڵ�C���������ߵĶԳ������������ཻ�ڵ�P����ֱ��BC�ཻ�ڵ�M������PB��
��1�����C�����Լ��������ߵĹ�ϵʽ��
��2������AC����x���·������������е�D��ʹS��ABD=S��ABC�����D�����ꣻ
��3�����������Ƿ���ڵ�Q��ʹ��QMB���PMB�������ȣ������ڣ�ֱ��д����Q�����ꣻ�������ڣ�˵�����ɣ�
��4���ڵ�һ���ޡ��Գ����Ҳ�����������Ƿ����һ��R��ʹ��RPM���RMB�������ȣ������ڣ�ֱ��д����R�����ꣻ�������ڣ�˵�����ɣ�
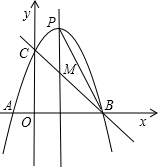
�⣺��1����A��-1��0����B ��3��0������y=ax2+bx+3�ã�
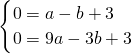 ��
��
��ã�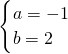 ��
��
����κ���ʽΪy=-x2+2x+3��
��x=0����y=3������C�������ǣ�0��3����
��2���ɣ�1����֪��D������Ϊ��x��-x2+2x+3����
��AB=4��OC=3��
��S��ABC= ��4��3=6��
��4��3=6��
��S��ABD=S��ABC��
�� •AB•|-x2+2x+3|=6��
•AB•|-x2+2x+3|=6��
��D��x���·����������ϣ�
��D�������ǣ�1�� ��3����
��3����
��3����y=-x2+2x+3=-��x-1��2+4��
��P��1��4�������������������ͼ1��
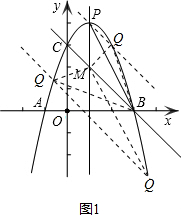
����B��C���������֪��ֱ��BC����ʽΪy=-x+3��
�����P��ֱ��BCƽ�е�ֱ��Ϊ��y=-x+b��
����P��1��4�����룬��y=-x+5��
��ֱ��BC���������߽���ʽ�Ƿ��н⣬������ڵ�Q��
���ɵã�-x2+2x+3=-x+5��
�⣺x=1��x=2��
����ֱ����õ㣨1��4����2��3����
��֪��P��1��4����
���Ե�Q��2��3����
���ɶԳ��ἰֱ��BC����ʽ��֪M��1��2����PM=2��
���P�䣨1��0������BCƽ�е�ֱ��Ϊy=-x+c��
��P����룬��y=-x+1��
����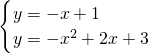 ��
��
��ã�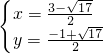 ��
��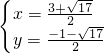 ��
��
�ʿɵô���Q��������Ϊ��2��3����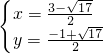 ��
��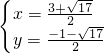 ��
��
��4���ɣ�2���ɵã�M��1��2������ͼ2��
�ɵ�M��P�������֪��R���ڣ�������Mƽ����x���ֱ�ߣ�
��ɵ�-x2+2x+3=2��
���x1=1- ���ڶԳ������࣬��ȥ����x2=1+
���ڶԳ������࣬��ȥ����x2=1+ ��
��
����R��1+ ��2����
��2����
��������1����A��-1��0����B ��3��0��������������y=ax2+bx+3�������a��b��ֵ��������������ߵĽ���ʽ����x=0�����C������ꣻ
��2���ɣ�1����֪��D������Ϊ��x��-x2+2x+3��������֪��������S��ABC�����ҡ�ABD�ĸ�ΪD��������ľ���ֵ�����Կɽ����������x��ֵ���ɣ�
��3����Ϊ�������εĵױ�MB��ͬ������ֻ������MB�ϵĸ���ȼ����������⣻
��4������ǰ������ɵó���M��PP'���е㣬�Ӷ�����M��x���ƽ���ߣ��������ߵĽ��㼴Ϊ����
�������������ڶ��κ����ۺ��⣬�漰�˴���ϵ������������ʽ��һԪ���η��̵Ľ⼰�����ε�������ۺ��Խ�ǿ���������ѵ��ڵ����ʣ��ؼ��Ǹ��ݵ�M��PP'���е���⣬�ѶȽϴ�
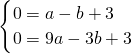 ��
��
��ã�
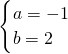 ��
������κ���ʽΪy=-x2+2x+3��
��x=0����y=3������C�������ǣ�0��3����
��2���ɣ�1����֪��D������Ϊ��x��-x2+2x+3����
��AB=4��OC=3��
��S��ABC=
 ��4��3=6��
��4��3=6����S��ABD=S��ABC��
��
 •AB•|-x2+2x+3|=6��
•AB•|-x2+2x+3|=6����D��x���·����������ϣ�
��D�������ǣ�1��
 ��3����
��3������3����y=-x2+2x+3=-��x-1��2+4��
��P��1��4�������������������ͼ1��

����B��C���������֪��ֱ��BC����ʽΪy=-x+3��
�����P��ֱ��BCƽ�е�ֱ��Ϊ��y=-x+b��
����P��1��4�����룬��y=-x+5��
��ֱ��BC���������߽���ʽ�Ƿ��н⣬������ڵ�Q��
���ɵã�-x2+2x+3=-x+5��
�⣺x=1��x=2��
����ֱ����õ㣨1��4����2��3����
��֪��P��1��4����
���Ե�Q��2��3����
���ɶԳ��ἰֱ��BC����ʽ��֪M��1��2����PM=2��
���P�䣨1��0������BCƽ�е�ֱ��Ϊy=-x+c��
��P����룬��y=-x+1��
����
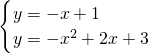 ��
����ã�
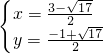 ��
��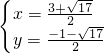 ��
���ʿɵô���Q��������Ϊ��2��3����
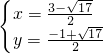 ��
��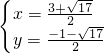 ��
����4���ɣ�2���ɵã�M��1��2������ͼ2��
�ɵ�M��P�������֪��R���ڣ�������Mƽ����x���ֱ�ߣ�

��ɵ�-x2+2x+3=2��
���x1=1-
 ���ڶԳ������࣬��ȥ����x2=1+
���ڶԳ������࣬��ȥ����x2=1+ ��
������R��1+
 ��2����
��2������������1����A��-1��0����B ��3��0��������������y=ax2+bx+3�������a��b��ֵ��������������ߵĽ���ʽ����x=0�����C������ꣻ
��2���ɣ�1����֪��D������Ϊ��x��-x2+2x+3��������֪��������S��ABC�����ҡ�ABD�ĸ�ΪD��������ľ���ֵ�����Կɽ����������x��ֵ���ɣ�
��3����Ϊ�������εĵױ�MB��ͬ������ֻ������MB�ϵĸ���ȼ����������⣻
��4������ǰ������ɵó���M��PP'���е㣬�Ӷ�����M��x���ƽ���ߣ��������ߵĽ��㼴Ϊ����
�������������ڶ��κ����ۺ��⣬�漰�˴���ϵ������������ʽ��һԪ���η��̵Ľ⼰�����ε�������ۺ��Խ�ǿ���������ѵ��ڵ����ʣ��ؼ��Ǹ��ݵ�M��PP'���е���⣬�ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
 ���㣬���ʵ�xΪ��ֵʱ���߶�CD�����ֵ�������ֵΪ���٣�
���㣬���ʵ�xΪ��ֵʱ���߶�CD�����ֵ�������ֵΪ���٣� OΪ����ԭ�㣬��������һ��C�ĺ�����Ϊ1��
OΪ����ԭ�㣬��������һ��C�ĺ�����Ϊ1�� ���������ϣ��������Ϊ12��
���������ϣ��������Ϊ12�� ��x�ύ�ڵ�A��B����A������Ϊ��-2��0����
��x�ύ�ڵ�A��B����A������Ϊ��-2��0����