Question

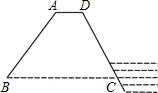
乐清市钟前水库大坝截面的迎水坡坡比（DE与AE的长度之比）为1：0.6，背水坡坡比为1：2，大坝高DE=50米，坝顶宽CD=7米，求大坝的截面的周长（精确到0.01）．

Answer 1

分析：先根据两个坡比求出AE和BF的长，然后利用勾股定理求出AD和BC，再由大坝的截面的周长=DC+AD+AB+BC可得出答案．

解答：解：∵迎水坡坡比（DE与AE的长度之比）为1：0.6，DE=50m，
即

DE

AE

=

1

0.6

，
∴AE=0.6DE=30（m），
在Rt△ADE中，AD=

DE2+AE2

=10

34

（m），
∵背水坡坡比为1：2，CF=DE=50m，
即

CF

BF

=

1

2

，
∴BF=100m，
在Rt△BCF中，BC=

CF2+BF2

=50

5

米，
∵EF=CD=7m，
∴AB=AE+EF+BF=30+7+100=137（m），
∴DC+AD+AB+BC=7+10

34

+137+50

5

≈264.11（m）．
∴大坝的截面的周长约为264.11m．

点评：本题考查了坡度和坡比问题与勾股定理的应用．注意利用三角函数求得梯形的各边长，理解坡比所表示的意义是解答本题关键．