Question

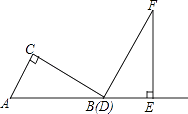
【题目】已知△OAB在直角坐标系中的位置如图，点A在第一象限，点B在x轴正半轴上，OA=OB=6，∠AOB=30°．

（1）求点A、B的坐标；
（2）开口向上的抛物线经过原点O和点B，设其顶点为E，当△OBE为等腰直角三角形时，求抛物线的解析式；
（3）设半径为2的⊙P与直线OA交于M、N两点，已知MN=2 ，P（m，2）（m＞0），求m的值．

Answer 1

【答案】
（1）

解：如图1 ，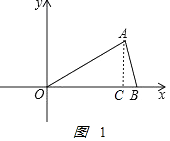

作 AC⊥OB于C点，

由OB=OA=6，得B点坐标为（6，0），

由OB=OA=6，∠AOB=30°，得

AC= OA=3，OC=OAcos∠AOC= OA=3 ，

∴A点坐标为（3 ，3）；

（2）

解：如图2 ，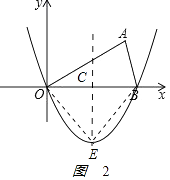

由其顶点为E，当△OBE为等腰直角三角形，得

OC=BC=CE= OB=3，

即E点坐标为（3，﹣3）．

设抛物线的解析式为y=a（x﹣3）2﹣3，将B点坐标代入，解得

a= ，

抛物线的解析式为y= （x﹣3）2﹣3

化简得y= x2﹣2x；

（3）

解：如图3 ，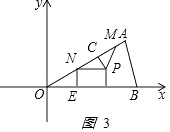

PN=2，CN= ，PC=1，

∠CNP=∠AOB=30°，

NP∥OB，

NE=2，得ON=4，

由勾股定理，得

OE= =2 ，即N（2 ，2）．

N向右平移2个单位得P（2 +2，2），

N向左平移2个单位，得P（2 ﹣2，2），

m的值为2 +2或2 ﹣2．

【解析】（1）根据30°的角所对的直角边是斜边的一半，可得AC的长，再根据锐角三角函数，可得OC，根据点的坐标，可得答案；（2）根据等腰直角三角形，可得E点坐标，再根据待定系数法，可得答案；（3）根据30°的角所对的直角边是斜边的一半，可得∠CNP=30°，再根据勾股定理OE的长，根据点的坐标，可得N点坐标，根据点的左右平移，可得P点坐标．