题目内容
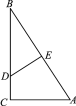
如图，有一张直角三角形纸片，两直角边AC＝6cm，BC＝8cm，将△ABC折叠，使点B与点A重合，折痕为DE，则CD等于( )
A.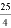 
cm B. 
cm C. 
cm D. 
cm
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
如图，有一张直角三角形纸片，两直角边AC＝6cm，BC＝8cm，将△ABC折叠，使点B与点A重合，折痕为DE，则CD等于( )
A. 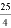cm B. cm C. cm D. cm
阅读快车系列答案
总有实数根．
+|3﹣x|的正确结果是__．
B. 
C. 9 D. 
与x轴、y轴分别交于点D、E，交OB于点F. 
B. 
C. 
D. 