题目内容
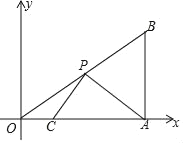
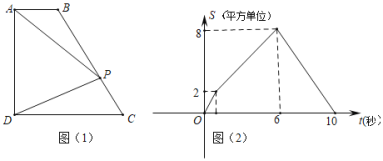
【题目】如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△PAD的面积为( )
A. 4B. 5C. 6D. 7
【答案】B
【解析】
根据函数图象和三角形面积得出AB+BC=6,CD=4,AD=4,AB=1,当P运动到BC中点时,梯形ABCD的中位线也是△APD的高,求出梯形ABCD的中位线长,再代入三角形面积公式即可得出结果.
解:根据题意得:四边形ABCD是梯形,AB+BC=6,CD=10-6=4,
∵![]() AD×CD=8,
AD×CD=8,
∴AD=4,
又∵![]() AD×AB=2,
AD×AB=2,
∴AB=1,
当P运动到BC中点时,梯形ABCD的中位线也是△APD的高,
∵梯形ABCD的中位线长=![]() (AB+CD)=
(AB+CD)=![]() ,
,
∴△PAD的面积![]()
故选:B.

练习册系列答案
相关题目