Question

（2013•东阳市模拟）平面直角坐标中，直线OA、OB都经过第一象限（O是坐标原点），且满足∠AOB=45°，如直线OA的解析式为y=kx，现探究直线OB解析式情况．

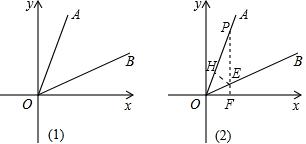
（1）当∠BOX=30°时（如图1），求直线OB解析式；
（2）当k=2时（如图2），探究过程：OA上取一点P（1，2）作PF⊥x轴于F，交OB于E，作EH⊥OA于H，则

OH

PH

=

1

2

，根据以上探究过程，请求出直线OB解析式；
（3）设直线OB解析式为y=mx，则m=

k-1

k+1

（k＞1）或

k+1

1-k

（0＜k＜1）

（用k表示），如双曲线y=

n

x

交OA于M，交OB于N，当OM=ON时，求k的值．

Answer 1

分析：（1）在OB上任取一点C，作CD⊥x轴与点D，设CD=a，由勾股定理可以得出OD=

3

a，设OB的解析式为y=kx，运用待定系数法就可以求出结论；
（2）由条件和勾股定理可以求出E点的坐标就可以求出OB的解析式；
（3）分k＞1时，0＜k＜1时，两种情况用k表示出m；分k＞1时，0＜k＜1时，两种情况求出k的值．

解答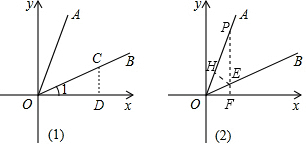：解：（1）在OB上任取一点C，作CD⊥x轴与点D，设CD=a，
∵∠1=30°，
∴OC=2CD=2a，
在Rt△ODC中，由勾股定理，得
OD=

3

a，
设OB的解析式为y=kx，由题意，得
a=

3

ak，
k=

3

3

．
∴OB的解析式为：y=

3

3

x；

（2）∵PF⊥x轴，P（1，2），
∴OF=1，PF=2，
∴由勾股定理，得
OP=

5

．
∴tan∠OPF=

1

2

．
∵EH⊥OA，
∴∠EHP=90°，
∴

EH

PH

=

1

2

，
设EH=x，PH=2x，
∴PE=

5

x
∴OH=

5

-2x．
∵∠HOE=45°，
∴OH=EH=x，
∴x=

5

-2x，

OH

PH

=

1

2

．
∴x=

5

3

∴AE=

5

3

，
∴EF=

1

3

∴E（1，

1

3

）．
设OB的解析式为y=k₁x，由题意，得
k₁=

1

3

．
∴OB的解析式为y=

1

3

x；

（3）k＞1时，同上可得m=

k-1

k+1

，
0＜k＜1时，m=

k+1

1-k

k＞1时，设M（1，k），则N（k，1），代入y=

k-1

k+1

x可得，k²-2k-1=0，k=

2

+1；
0＜k＜1时，同理可得k=

2

-1．
故答案为：

1

2

；

k-1

k+1

（k＞1）或

k+1

1-k

（0＜k＜1）．

点评：考查了一次函数综合题，涉及的知识点有：勾股定理，待定系数法，三角函数，分类思想和方程思想的运用，综合性较强，有一定的难度．