题目内容
（2012•安庆二模）如图，在平面直角坐标系中，点P在第一象限，⊙P与x轴相切于点Q、与y轴相交于点M（0，4）和N（0，16），则点P的坐标是（8，10）
（8，10）
．分析：首先连接PQ，PN，作点P作PH⊥MN于H，由点M（0，4）和N（0，16），利用垂径定理，可得MH=HH=6，即可得PQ=MH=10，又由勾股定理，即可求得PH的长，继而可得点P的坐标．
解答：
解：连接PQ，PN，作点P作PH⊥MN于H，
∵M（0，4），N（0，16），
∴ON=16，OM=4，
∴MN=16-4=12，
∴MH=NH=
MN=6，
∴PQ=OH=OM+MH=4+6=10，
∴PN=10，
在Rt△PNH中，PH=
=8，
∴点P的坐标是（8，10）．
故答案为：（8，10）．
解：连接PQ，PN，作点P作PH⊥MN于H，∵M（0，4），N（0，16），
∴ON=16，OM=4，
∴MN=16-4=12，
∴MH=NH=
| 1 |
| 2 |
∴PQ=OH=OM+MH=4+6=10，
∴PN=10，
在Rt△PNH中，PH=
| PN2-NH2 |
∴点P的坐标是（8，10）．
故答案为：（8，10）．
点评：此题考查了切线的性质、垂径定理以及勾股定理．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
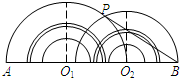（2012•安庆二模）如图，大小两个量角器的零度线都在直线AB上，而且小量角器的中心在大量角器的外边缘上．如果它们外边缘上的公共点P在大量角器上对应的度数为50°，那么∠PBA为的度数（ ）
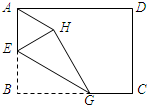（2012•安庆二模）如图，已知矩形纸片ABCD，E是AB边的中点，点G为BC边上的一点，现沿EG将纸片折叠，使点B落在纸片上的点H处，连接AH．若AB=EG，则与∠BEG相等的角的个数为（ ）