题目内容
化简求值: ,其中
,其中 .
.
解:∵a=2+ >0,b=2-
>0,b=2- >0,
>0,
∴a+b=4,ab=1,
∴原式= +
+
=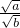 +
+
= +
+
=
 ,
,
当a+b=4,ab=1,原式=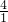 ×
× =4.
=4.
分析:由a=2+ ,b=2-
,b=2- ,得到a+b=4,ab=1,且a>0,b>0,再把代数式利用因式分解的方法得到原式=
,得到a+b=4,ab=1,且a>0,b>0,再把代数式利用因式分解的方法得到原式= +
+ ,约分后得
,约分后得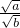 +
+ ,接着分母有理化和通分得到原式=
,接着分母有理化和通分得到原式=
 ,然后根据整体思想进行计算.
,然后根据整体思想进行计算.
点评:本题考查了二次根式的化简求值:先把各二次根式化为最简二次根式,再合并同类二次根式,然后把字母的值代入(或整体代入)进行计算.
 >0,b=2-
>0,b=2- >0,
>0,∴a+b=4,ab=1,
∴原式=
 +
+
=
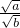 +
+
=
 +
+
=

 ,
,当a+b=4,ab=1,原式=
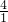 ×
× =4.
=4.分析:由a=2+
 ,b=2-
,b=2- ,得到a+b=4,ab=1,且a>0,b>0,再把代数式利用因式分解的方法得到原式=
,得到a+b=4,ab=1,且a>0,b>0,再把代数式利用因式分解的方法得到原式= +
+ ,约分后得
,约分后得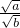 +
+ ,接着分母有理化和通分得到原式=
,接着分母有理化和通分得到原式=
 ,然后根据整体思想进行计算.
,然后根据整体思想进行计算.点评:本题考查了二次根式的化简求值:先把各二次根式化为最简二次根式,再合并同类二次根式,然后把字母的值代入(或整体代入)进行计算.

练习册系列答案
相关题目
 ,其中
,其中 、
、
 的解与方程2x-1=3的解相同,求m的值
的解与方程2x-1=3的解相同,求m的值 ②
② 
 ,其中
,其中 ,
,