题目内容
 如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内
如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内 上一点,∠BMO=120°,则⊙C的半径长为
上一点,∠BMO=120°,则⊙C的半径长为
- A.6
- B.5
- C.3
- D.3

C
分析:先根据圆内接四边形的性质求出∠OAB的度数,由圆周角定理可知∠AOB=90°,故可得出∠ABO的度数,根据直角三角形的性质即可得出AB的长,进而得出结论.
解答:∵四边形ABMO是圆内接四边形,∠BMO=120°,
∴∠BAO=60°,
∵AB是⊙O的直径,
∴∠AOB=90°,
∴∠ABO=90°-∠BAO=90°-60°=30°,
∵点A的坐标为(0,3),
∴OA=3,
∴AB=2OA=6,
∴⊙C的半径长= =3.
=3.
故选C.
点评:本题考查的是圆内接四边形的性质、圆周角定理及直角三角形的性质,熟知圆内接四边形对角互补的性质是解答此题的关键.
分析:先根据圆内接四边形的性质求出∠OAB的度数,由圆周角定理可知∠AOB=90°,故可得出∠ABO的度数,根据直角三角形的性质即可得出AB的长,进而得出结论.
解答:∵四边形ABMO是圆内接四边形,∠BMO=120°,
∴∠BAO=60°,
∵AB是⊙O的直径,
∴∠AOB=90°,
∴∠ABO=90°-∠BAO=90°-60°=30°,
∵点A的坐标为(0,3),
∴OA=3,
∴AB=2OA=6,
∴⊙C的半径长=
 =3.
=3.故选C.
点评:本题考查的是圆内接四边形的性质、圆周角定理及直角三角形的性质,熟知圆内接四边形对角互补的性质是解答此题的关键.

练习册系列答案
相关题目
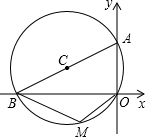 (2012•深圳)如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内
(2012•深圳)如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内
 如图,⊙C过原点,且与两坐标轴分别交于点A和点B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径长为
如图,⊙C过原点,且与两坐标轴分别交于点A和点B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径长为 上一点,∠BM0=120o,则⊙C的半径长为【 】
上一点,∠BM0=120o,则⊙C的半径长为【 】

 上一点,∠BMO=120°,则⊙C的半径长为( )
上一点,∠BMO=120°,则⊙C的半径长为( )
