题目内容
 (2012•南充)如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=
(2012•南充)如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=| 3 | 4 |
(1)求抛物线的函数解析式;
(2)直线m与⊙C相切于点A,交y轴于点D.动点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动;点P的速度为每秒一个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD时,求运动时间t的值;
(3)点R在抛物线位于x轴下方部分的图象上,当△ROB面积最大时,求点R的坐标.
分析:(1)根据抛物线y=ax2+bx经过点A(4,0)与点(-2,6),利用待定系数法求抛物线解析式;
(2)如答图1,由已知条件,可以计算出OD、AE等线段的长度.当PQ⊥AD时,过点O作OF⊥AD于点F,此时四边形OFQP、OFAE均为矩形.则在Rt△ODF中,利用勾股定理求出DF的长度,从而得到时间t的数值;
(3)因为OB为定值,欲使△ROB面积最大,只需OB边上的高最大即可.按照这个思路解决本题.
如答图2,当直线l平行于OB,且与抛物线相切时,OB边上的高最大,从而△ROB的面积最大.联立直线l和抛物线的解析式,利用一元二次方程判别式等于0的结论可以求出R点的坐标.
(2)如答图1,由已知条件,可以计算出OD、AE等线段的长度.当PQ⊥AD时,过点O作OF⊥AD于点F,此时四边形OFQP、OFAE均为矩形.则在Rt△ODF中,利用勾股定理求出DF的长度,从而得到时间t的数值;
(3)因为OB为定值,欲使△ROB面积最大,只需OB边上的高最大即可.按照这个思路解决本题.
如答图2,当直线l平行于OB,且与抛物线相切时,OB边上的高最大,从而△ROB的面积最大.联立直线l和抛物线的解析式,利用一元二次方程判别式等于0的结论可以求出R点的坐标.
解答:解:(1)∵抛物线y=ax2+bx经过点A(4,0)与点(-2,6),
∴
,解得
∴抛物线的解析式为:y=
x2-2x.
(2) 如答图1,连接AC交OB于点E,由垂径定理得AC⊥OB.
如答图1,连接AC交OB于点E,由垂径定理得AC⊥OB.
∵AD为切线,∴AC⊥AD,
∴AD∥OB.
过O点作OF⊥AD于F,
∴四边形OFAE是矩形,
∵tan∠AOB=
,∴sin∠AOB=
,
∴AE=OA•sin∠AOB=4×
=2.4,
OD=OA•tan∠OAD=OA•tan∠AOB=4×
=3.
当PQ⊥AD时,OP=t,DQ=2t.
过O点作OF⊥AD于F,则在Rt△ODF中,
OD=3,OF=AE=2.4,DF=DQ-FQ=DQ-OP=2t-t=t,
由勾股定理得:DF=
=
=1.8,
∴t=1.8秒;
(3)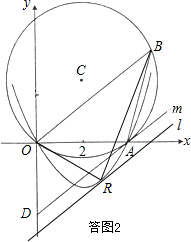 如答图2,设直线l平行于OB,且与抛物线有唯一交点R(相切),
如答图2,设直线l平行于OB,且与抛物线有唯一交点R(相切),
此时△ROB中OB边上的高最大,所以此时△ROB面积最大.
∵tan∠AOB=
,∴直线OB的解析式为y=
x,
由直线l平行于OB,可设直线l解析式为y=
x+b.
∵点R既在直线l上,又在抛物线上,
∴
x2-2x=
x+b,化简得:2x2-11x-4b=0.
∵直线l与抛物线有唯一交点R(相切),
∴判别式△=0,即112+32b=0,解得b=-
,
此时原方程的解为x=
,即xR=
,
而yR=
xR2-2xR=-
∴点R的坐标为R(
,-
).
∴
|
|
∴抛物线的解析式为:y=
| 1 |
| 2 |
(2)
 如答图1,连接AC交OB于点E,由垂径定理得AC⊥OB.
如答图1,连接AC交OB于点E,由垂径定理得AC⊥OB.∵AD为切线,∴AC⊥AD,
∴AD∥OB.
过O点作OF⊥AD于F,
∴四边形OFAE是矩形,
∵tan∠AOB=
| 3 |
| 4 |
| 3 |
| 5 |
∴AE=OA•sin∠AOB=4×
| 3 |
| 5 |
OD=OA•tan∠OAD=OA•tan∠AOB=4×
| 3 |
| 4 |
当PQ⊥AD时,OP=t,DQ=2t.
过O点作OF⊥AD于F,则在Rt△ODF中,
OD=3,OF=AE=2.4,DF=DQ-FQ=DQ-OP=2t-t=t,
由勾股定理得:DF=
| OD2-OF2 |
| 32-2.42 |
∴t=1.8秒;
(3)
 如答图2,设直线l平行于OB,且与抛物线有唯一交点R(相切),
如答图2,设直线l平行于OB,且与抛物线有唯一交点R(相切),此时△ROB中OB边上的高最大,所以此时△ROB面积最大.
∵tan∠AOB=
| 3 |
| 4 |
| 3 |
| 4 |
由直线l平行于OB,可设直线l解析式为y=
| 3 |
| 4 |
∵点R既在直线l上,又在抛物线上,
∴
| 1 |
| 2 |
| 3 |
| 4 |
∵直线l与抛物线有唯一交点R(相切),
∴判别式△=0,即112+32b=0,解得b=-
| 121 |
| 32 |
此时原方程的解为x=
| 11 |
| 4 |
| 11 |
| 4 |
而yR=
| 1 |
| 2 |
| 55 |
| 32 |
∴点R的坐标为R(
| 11 |
| 4 |
| 55 |
| 32 |
点评:本题是二次函数综合题,主要考查了二次函数的图形与性质、待定系数法求函数解析式、一元二次方程根的判别式、圆、勾股定理和解直角三角形等重要知识点.难点在于第(3)问,判定何时△ROB的面积最大是解决问题的关键.本题覆盖知识面广,难度较大,同学们只有做到基础扎实和灵活运用才能够顺利解答.
本题第(3)问亦可利用二次函数极值的方法解决,同学们有兴趣可深入探讨.
本题第(3)问亦可利用二次函数极值的方法解决,同学们有兴趣可深入探讨.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•南充)如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积为24cm2,则AC长是
(2012•南充)如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积为24cm2,则AC长是 (2012•南充模拟)如图,有一块半圆形钢板,直径AB=20cm,计划将此钢板切割成下底为AB的等腰梯形,上底CD的端点在圆周上,且CD=10cm.求图中阴影部分的面积.
(2012•南充模拟)如图,有一块半圆形钢板,直径AB=20cm,计划将此钢板切割成下底为AB的等腰梯形,上底CD的端点在圆周上,且CD=10cm.求图中阴影部分的面积. (2012•南充)如图,平面直角坐标系中,⊙O的半径长为1,点P(a,0),⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,a的值为( )
(2012•南充)如图,平面直角坐标系中,⊙O的半径长为1,点P(a,0),⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,a的值为( ) (2012•南充)如图,把一个圆形转盘按1:2:3:4的比例分成A、B、C、D四个扇形区域,自由转动转盘,停止后指针落在B区域的概率为
(2012•南充)如图,把一个圆形转盘按1:2:3:4的比例分成A、B、C、D四个扇形区域,自由转动转盘,停止后指针落在B区域的概率为