题目内容
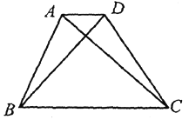
【题目】如图,菱形![]() 中,
中,![]() 于
于![]() ,交
,交![]() 于F,
于F,![]() 于
于![]() ,若
,若![]() 的周长为4,则菱形
的周长为4,则菱形![]() 的面积为( ).
的面积为( ).

A.![]() B.
B.![]() C.16D.
C.16D.![]()
【答案】B
【解析】
由菱形的性质得到∠BCD=45°,推出△BFG与△BEC是等腰直角三角形,根据全等三角形的性质得到FG=FE,CG=CE,设BG=FG=EF=x,得到BF=![]() x,根据△BFG的周长为4,列方程x+x+
x,根据△BFG的周长为4,列方程x+x+![]() x=4,即可得到结论.
x=4,即可得到结论.
∵菱形ABCD中,∠D=135°,
∴∠BCD=45°,
∵BE⊥CD于E,FG⊥BC于G,
∴△BFG与△BEC是等腰直角三角形,
∵∠GCF=∠ECF,∠CGF=∠CEF=90°,
CF=CF,
∴△CGF≌△CEF(AAS),
∴FG=FE,CG=CE,
设BG=FG=EF=x,
∴BF=![]() x,
x,
∵△BFG的周长为4,
∴x+x+![]() x=4,
x=4,
∴x=4-2![]() ,
,
∴BE=2![]() ,
,
∴BC=![]() BE=4,
BE=4,
∴菱形ABCD的面积=4×2![]() =8
=8![]() ,
,
故选:B.

练习册系列答案
相关题目
【题目】某弹簧的长度与所挂物体质量之间的关系如下表:
所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度/厘米 | 10 | 10.4 | 10.8 | 11.2 | 11.6 | 12 |
(1)如果所挂物体的质量用x表示,弹簧的长度用y表示,请直接写出y与x满足的关系式.
(2)当所挂物体的质量为10千克时,弹簧的长度是多少?