题目内容
【题目】如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3 ![]() ,则GH= .
,则GH= . 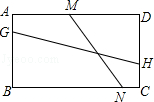
【答案】3 ![]()
【解析】解:如图,过点A作AE∥GH交CD于E,作AF∥MN交BC于F, 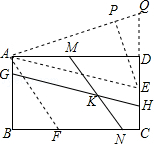
则AF=MN=3 ![]() ,AE=GH,
,AE=GH,
∵∠GKM=45°,
∴∠BAF+∠DAE=90°﹣45°=45°,
作∠QAE=45°交CD的延长线于Q,
则∠QAD+∠DAE=45°,
∴∠QAD=∠FAB,
∵∠B=∠ADQ=90°,
∴△ABF∽△AQD,
∴ ![]() ,
,
∴ ![]() ,
,
∴AQ= ![]() ,
,
在Rt△ADQ中,DQ= ![]() =
= ![]() ,
,
过点E作EP⊥AQ于P,
∵∠QAE=45°,
∴△AEP是等腰直角三角形,
设GH=AE=x,则AP=EP= ![]() AE=
AE= ![]() x,
x,
∵tan∠Q= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得x=3 ![]() ,
,
所以GH=3 ![]() .
.
故答案为:3 ![]() .
.
过点A作AE∥GH交CD于E,作AF∥MN交BC于F,于是得到AF=MN=3 ![]() ,AE=GH,由于∠GKM=45°,得到∠BAF+∠DAE=90°﹣45°=45°,作∠QAE=45°交CD的延长线于Q,推出∠QAD+∠DAE=45°,通过△ABF≌△AQD,根据相似三角形的性质得到
,AE=GH,由于∠GKM=45°,得到∠BAF+∠DAE=90°﹣45°=45°,作∠QAE=45°交CD的延长线于Q,推出∠QAD+∠DAE=45°,通过△ABF≌△AQD,根据相似三角形的性质得到 ![]() ,求得AQ=
,求得AQ= ![]() ,在Rt△ADQ中,由勾股定理得到DQ=
,在Rt△ADQ中,由勾股定理得到DQ= ![]() =
= ![]() ,过点E作EP⊥AQ于P,得到△AEP是等腰直角三角形,设GH=AE=x,则AP=EP=
,过点E作EP⊥AQ于P,得到△AEP是等腰直角三角形,设GH=AE=x,则AP=EP= ![]() AE=
AE= ![]() ,然后利用∠Q的正切值列出方程求解即可.
,然后利用∠Q的正切值列出方程求解即可.

练习册系列答案
相关题目