题目内容
如图所示:请按照要求解答问题:
(1)数轴上的点C在2、3的中点位置,则C表示的数是
(2)求线段AB的中点D与线段BC的中点E的距离DE;
(3)在数轴上方有一点M,下方有一点N,且∠ABM=120°,∠CBN=60°,请画出示意图,并判断BC能否平分∠MBN?并简要说明理由.
(1)数轴上的点C在2、3的中点位置,则C表示的数是
2.5
2.5
,线段AB的中点D表示的数是-2
-2
.
(2)求线段AB的中点D与线段BC的中点E的距离DE;
(3)在数轴上方有一点M,下方有一点N,且∠ABM=120°,∠CBN=60°,请画出示意图,并判断BC能否平分∠MBN?并简要说明理由.
分析:(1)直接从数轴上读数即可;
(2)先求BC的中点E表示的数:(-1+2.5)÷2=0.75,再求DE的长;
(3)实际是以AB为边,在数轴上方画∠ABM=120°,下方画∠CBN=60°,根据平角的定义可求出∠MBC=60°,所以BC平分∠MBN.
(2)先求BC的中点E表示的数:(-1+2.5)÷2=0.75,再求DE的长;
(3)实际是以AB为边,在数轴上方画∠ABM=120°,下方画∠CBN=60°,根据平角的定义可求出∠MBC=60°,所以BC平分∠MBN.
解答:解:(1)读数轴可知,C表示的数是2.5,线段AB的中点D表示的数是-2;
(2)线段BC的中点E表示的数是:(-1+2.5)÷2=0.75
∴DE=2+0.75=2.75;
(3)如图 ,BC平分∠MBN.
,BC平分∠MBN.
理由是:
∵∠ABM=120°,
∴∠MBC=180°-∠ABM=180°-120°=60°,
又∵∠CBN=60°,
∴∠MBC=∠CBN,
即BC平分∠MBN.
(2)线段BC的中点E表示的数是:(-1+2.5)÷2=0.75
∴DE=2+0.75=2.75;
(3)如图
 ,BC平分∠MBN.
,BC平分∠MBN.理由是:
∵∠ABM=120°,
∴∠MBC=180°-∠ABM=180°-120°=60°,
又∵∠CBN=60°,
∴∠MBC=∠CBN,
即BC平分∠MBN.
点评:此题主要借助数轴考查了两点的距离、角平分线的定义等知识点,要灵活解决.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
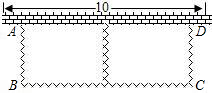 花圃.设花圃的边AB长为x,花圃的面积为s米2.
花圃.设花圃的边AB长为x,花圃的面积为s米2.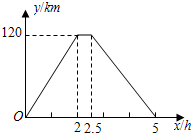 (1)一辆经营长途运输的货车在高速公路A处加满油后匀速行驶,下表记录的是货车一次加满油后油箱内余油y(升)与行驶时间x(时)之间的关系:
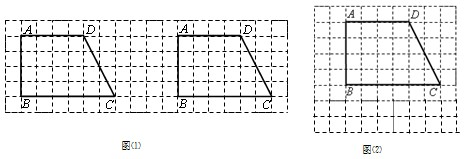
(1)一辆经营长途运输的货车在高速公路A处加满油后匀速行驶,下表记录的是货车一次加满油后油箱内余油y(升)与行驶时间x(时)之间的关系: 24、在单位长度为1的正方形网格中建立直角坐标系,如图所示.已知点A,B,C的坐标分别为(0,0),(4,0),(6,2).
24、在单位长度为1的正方形网格中建立直角坐标系,如图所示.已知点A,B,C的坐标分别为(0,0),(4,0),(6,2).