题目内容
 如图所示,已知△ABC,用尺规作一点D,使四边形ABDC是平行四边形,作图的方法(判定平行四边形依据相同的方法算同一种作图)有( )
如图所示,已知△ABC,用尺规作一点D,使四边形ABDC是平行四边形,作图的方法(判定平行四边形依据相同的方法算同一种作图)有( )| A、3种 | B、4种 | C、5种 | D、6种 |
考点:平行四边形的判定
专题:
分析:运用平行四边形的判定定理,作平行四边形ABDC,问题即可解决.
解答:解:运用尺规作一点D的方法有:
法1:作线段BC的垂直平分线,垂足为E,连接AE并延长到D,使AE=DE;若连接BD、CD,
则四边形ABDC为平行四边形,故点D即为所求作的点;
法2:过点B作BM∥AC,在BM上截取BD,使BD=AC;若连接DC,则四边形ABDC为平行四边形,故点D即为所求作的点;
法3:分别过点B、C作BD∥AC,CD∥AB,其交点为D,则四边形ABDC为平行四边形,故点D即为所求作的点;
法4:分别以点B、C为圆心,以AC、AB的长为半径化弧,两弧交于点D;若连接BD、CD,
则四边形ABDC为平行四边形,故点D即为所求作的点;
综上所述,运用尺规作一点D的方法有4种.
故选B.
法1:作线段BC的垂直平分线,垂足为E,连接AE并延长到D,使AE=DE;若连接BD、CD,
则四边形ABDC为平行四边形,故点D即为所求作的点;
法2:过点B作BM∥AC,在BM上截取BD,使BD=AC;若连接DC,则四边形ABDC为平行四边形,故点D即为所求作的点;
法3:分别过点B、C作BD∥AC,CD∥AB,其交点为D,则四边形ABDC为平行四边形,故点D即为所求作的点;
法4:分别以点B、C为圆心,以AC、AB的长为半径化弧,两弧交于点D;若连接BD、CD,
则四边形ABDC为平行四边形,故点D即为所求作的点;
综上所述,运用尺规作一点D的方法有4种.
故选B.
点评:该命题主要考查了平行四边形的判定及其应用问题;解题的关键是综合运用平行四边形的判定方法,灵活判断、解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
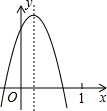 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: 如图是某公园一喷水池,在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25
如图是某公园一喷水池,在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25
 在△ABC中,AB=AC,点D在BA延长线上,点E在BC上,DC=DE,DE与AC相交于点F,且DF=FE,求证:BE=EC.
在△ABC中,AB=AC,点D在BA延长线上,点E在BC上,DC=DE,DE与AC相交于点F,且DF=FE,求证:BE=EC.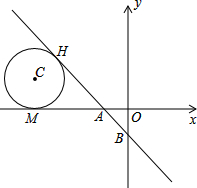 已知,平面直角坐标系中,直线ABy=-x-
已知,平面直角坐标系中,直线ABy=-x-