题目内容
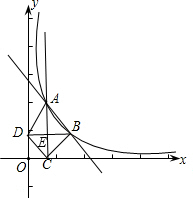 如图所示,在直角坐标系平面内,函数y=
如图所示,在直角坐标系平面内,函数y=| m |
| x |
(1)用含a的代数式表示E点的坐标;
(2)若△ABD的面积是4,求点B的坐标;
(3)当CD=
| 5 |
| 3 |
(4)求△ADE的面积与△CBE的面积的比值?
分析:(1)根据A点坐标可求得m的值,将B点坐标代入反比例函数的解析式中,即可得a、b的比例关系式,从而用a表示出点B的坐标,结合A、B两点的坐标即可求得点E的坐标.
(2)根据B点坐标,可得BD的长,根据A、E的坐标,可得AE的值,结合△BD的面积即可求得a的值,从而确定出点B的坐标.
(3)根据E点坐标,可表示出CE、DE的长,在Rt△DEC中,利用勾股定理和CD的长,即可求得a的值,从而确定点B的坐标.
(4)分别表示出两个三角形的面积,然后求它们的比值即可.
(2)根据B点坐标,可得BD的长,根据A、E的坐标,可得AE的值,结合△BD的面积即可求得a的值,从而确定出点B的坐标.
(3)根据E点坐标,可表示出CE、DE的长,在Rt△DEC中,利用勾股定理和CD的长,即可求得a的值,从而确定点B的坐标.
(4)分别表示出两个三角形的面积,然后求它们的比值即可.
解答:解:(1)∵函数y=
(x>0,m是常数)图象经过A(1,4),∴m=4;
据题意,可得B点的坐标为(a,
),D点的坐标为(0,
),E点的坐标为(1,
).
(2)∵a>1,∴DB=a,AE=4-
,
由△ABD的面积为4,即
a(4-
)=4,
解得a=3,∴点B的坐标为(3,
).
(3)当CD=
时,CD2=CE2+DE2,即(
)2=(
)2+12,
解得:a=3,此时B点的坐标为(3,
).
(4)
=
=1.
| m |
| x |
据题意,可得B点的坐标为(a,
| 4 |
| a |
| 4 |
| a |
| 4 |
| a |
(2)∵a>1,∴DB=a,AE=4-
| 4 |
| a |
由△ABD的面积为4,即
| 1 |
| 2 |
| 4 |
| a |
解得a=3,∴点B的坐标为(3,
| 4 |
| 3 |
(3)当CD=
| 5 |
| 3 |
| 5 |
| 3 |
| 4 |
| a |
解得:a=3,此时B点的坐标为(3,
| 4 |
| 3 |
(4)
| S△ADE |
| S△CBE |
| ||||
|
点评:此题主要考查了反比例函数解析式的确定、函数图象上点的坐标特征、勾股定理以及三角形面积的计算方法等知识,难度适中.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
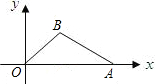 sin∠BOA=
sin∠BOA= 1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.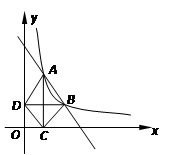

 的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.